 TAMPERE UNIVERSITY OF TECHNOLOGY
-
Department of Signal Processing
TAMPERE UNIVERSITY OF TECHNOLOGY
-
Department of Signal Processing
Forward/backward modeling |
Multi-plane phase retrieval |
Sparse reconstruction | Publications | Contacts | |||
|
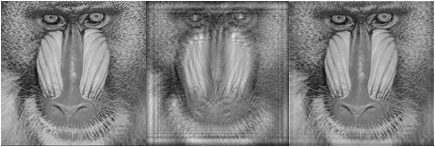
The wavefront reconstruction is formulated as an inverse problem where the complex exponent or the amplitude and phase of this exponent are assumed to admit sparse representations in suitable sparsifying transforms (dictionaries). The sparse modeling is a form of regularization of the inverse problem. For design of these overcomplete sparsifying dictionaries we use Block Matching 3D (BM3D) and learning dictionary techniques. Various optical setups (interferometric and non-interferometric) are considered with algorithms developed for Gaussian and Poissonian noise in intensity measurements.
The LASIP routines are available free-of-charge for educational and non-profit scientific research, enabling others researchers to understand and reproduce our work. Any unauthorized use of the LASIP routines for industrial or profit-oriented activities is expressively prohibited. Please read the LASIP limited license
|
|||||||
[1] V. Katkovnik and J. Astola, “High-accuracy wave field reconstruction: decoupled inverse imaging with sparse modeling of phase and amplitude,” J. Opt. Soc. Am. A 29, 44-54 (2012).
V. Katkovnik and J. Astola, “High-accuracy wave field reconstruction: decoupled inverse imaging with sparse modeling of phase and amplitude,” J. Opt. Soc. Am. A 29, 44-54 (2012).
[2] V. Katkovnik and J. Astola, “Phase retrieval via spatial light modulator phase modulation in 4f optical setup: numerical inverse imaging with sparse regularization for phase and amplitude,” J. Opt. Soc. Am. A 29, 105-116 (2012).
V. Katkovnik and J. Astola, “Phase retrieval via spatial light modulator phase modulation in 4f optical setup: numerical inverse imaging with sparse regularization for phase and amplitude,” J. Opt. Soc. Am. A 29, 105-116 (2012).
[3] A.Migukin, V. Katkovnik, and J. Astola, “Advanced phase retrieval: maximum likelihood technique with sparse regularization of phase and amplitude,” arXiv:1108.3251v1
A.Migukin, V. Katkovnik, and J. Astola, “Advanced phase retrieval: maximum likelihood technique with sparse regularization of phase and amplitude,” arXiv:1108.3251v1
[4] A.Migukin, V. Katkovnik, and J. Astola, “Advanced multi-plane phase retrieval using Graphic Processing Unit: augmented Lagrangian technique with sparse regularization,” Conf. SPIE 84291N (2012).
A.Migukin, V. Katkovnik, and J. Astola, “Advanced multi-plane phase retrieval using Graphic Processing Unit: augmented Lagrangian technique with sparse regularization,” Conf. SPIE 84291N (2012).
[5] V. Katkovnik and J. Astola, "Compressive sensing computational ghost imaging," J. Opt. Soc. Am. A 29, 1556-1567 (2012).
V. Katkovnik and J. Astola, "Compressive sensing computational ghost imaging," J. Opt. Soc. Am. A 29, 1556-1567 (2012).
[6] A. Migukin, M. Agour, and V. Katkovnik, "Phase retrieval in 4f optical system: background compensation and sparse regularization of object with binary amplitude," Appl. Opt. 52, A269-A280 (2013).
A. Migukin, M. Agour, and V. Katkovnik, "Phase retrieval in 4f optical system: background compensation and sparse regularization of object with binary amplitude," Appl. Opt. 52, A269-A280 (2013).
[7] V. Katkovnik and J. Astola, “Compressive ptychographical coherent diffractive imaging based on Poissonian maximum likelihood and sparse approximations for phase and magnitude,” J. Opt. Soc. Am. A, Vol. 30, Issue 3, pp. 367-379 (2013).
V. Katkovnik and J. Astola, “Compressive ptychographical coherent diffractive imaging based on Poissonian maximum likelihood and sparse approximations for phase and magnitude,” J. Opt. Soc. Am. A, Vol. 30, Issue 3, pp. 367-379 (2013).
[8] V. Katkovnik and J. Bioucas-Dias , \93Wavefront reconstruction in phase-shifting interferometry via sparse coding of amplitude and absolute phase,\94 J. Opt. Soc. Am. A, Vol. 31, No. 8 , August, pp. 1801-1810 (2014).
V. Katkovnik and J. Bioucas-Dias , \93Wavefront reconstruction in phase-shifting interferometry via sparse coding of amplitude and absolute phase,\94 J. Opt. Soc. Am. A, Vol. 31, No. 8 , August, pp. 1801-1810 (2014).
[9] V. Katkovnik, J. Bioucas-Dias, Hongxing Hao, \93Wavefront reconstruction from noisy fringe observations via sparse coding,\94 Proc. Fringe 2013: 7th International Workshop on Advanced Optical Imaging and Metrology, pp. 179-184 (2013).
V. Katkovnik, J. Bioucas-Dias, Hongxing Hao, \93Wavefront reconstruction from noisy fringe observations via sparse coding,\94 Proc. Fringe 2013: 7th International Workshop on Advanced Optical Imaging and Metrology, pp. 179-184 (2013).
[10] H. Hongxing, J. M. Bioucas-Dias, and V. Katkovnik, "Interferometric phase estimation via sparse coding in the complex domain", IEEE Transactions on Geoscience and Remote Sensing, Vol. 53, Issue. 5, pp. 2587-2602, 2015 (Matlab code)
H. Hongxing, J. M. Bioucas-Dias, and V. Katkovnik, "Interferometric phase estimation via sparse coding in the complex domain", IEEE Transactions on Geoscience and Remote Sensing, Vol. 53, Issue. 5, pp. 2587-2602, 2015 (Matlab code)
[11] V. Katkovnik, "Phase retrieval from noisy data based on sparse approximation of object phase and amplitude", 2017, https://arxiv.org/abs/1709.01071
V. Katkovnik, "Phase retrieval from noisy data based on sparse approximation of object phase and amplitude", 2017, https://arxiv.org/abs/1709.01071
[12] V. Katkovnik and K. Egiazarian, "Sparse phase imaging based on complex domain nonlocal BM3D techniques", Digital Signal Processing, Academic Press, 63:72-85, 2017.
V. Katkovnik and K. Egiazarian, "Sparse phase imaging based on complex domain nonlocal BM3D techniques", Digital Signal Processing, Academic Press, 63:72-85, 2017.
|
|
Please contact V. Katkovnik for additional information. |