When the rank of the autoregression matrix is unresticted, the maximum
likelihood estimator under normality is the least squares estimator. When
the rank is restricted, the maximum likelihood estimator (reduced rank
regression) is composed of the eigenvectors of the effect covariance matrix
in the metric of the error covariance matrix corresponding to the largest
eigenvalues (Anderson, 1951). The asymptotic distribution of these two
covariance matrices under normality is obtained and is used to derive the
asymptotic distribution of the eigenvectors and eigenvalues. These distributions
are different from those for independent (stochastic or nonstochastic)
regressors. The asymptotic distribution of the reduced rank regression
is the asymptotic distribution of the least squares estimator with some
restrictions; hence the covariance of the reduced rank regression is smaller
than that of the least squares estimator. This result does not depend on
normality although the asymptotic distribution of the eigenvectors and
eigenvalues does.
Keywords: Canonical correlations and vectors, eigenvalues
and eigenvectors, asymptotic distributions.
ILAS LECTURE
Computation of certain kinds of numerical quadratures on polygonal regions
of the plane and the reconstruction of these regions from their moments
can be viewed as dual problems. In fact, this is a consequence of a little-known
result of Motzkin and Schoenberg. In this talk, we discuss this result
and address the inverse problem of (uniquely) reconstructing a polygonal
region in the complex plane from a finite number of its complex moments.
Algorithms have been developed for polygon reconstruction from moments
and have been applied to tomographic image reconstruction problems. The
numerical computations involved in the algorithm can be very ill-conditioned.
We have managed to improve the algorithms used, and to recognize when the
problem will be ill-conditioned. Some numerical results will be given.
* Joint work with Peyman MILANFAR
(University of California, Santa Cruz, USA) and James VARAH
(University of British Columbia, Vancouver, Canada).
INVITED TALKS
The arithmetic-geometric mean inequality for positive numbers a, b > 0 or the Schwarz inequality for complex numbers x, y
is the most fundamental inequality. One of its generalization is the Young inequality
or
If scalars a, b are replaced with matrices A, B,
there is no problem in understanding ![]() as positive semi-definiteness of A and B. Correspondingly,
the order relation, Löwner order,
as positive semi-definiteness of A and B. Correspondingly,
the order relation, Löwner order, ![]() between two Hermitian matrices is induced by the cone of positive semi-definite
matrices.
between two Hermitian matrices is induced by the cone of positive semi-definite
matrices.
There are, however, several directions for matrix generalizations of the Schwarz inequality as well as the Young one. We take up two of them.
The first one is an approach using matrix inequalities, that is, to discuss the inequalities with respect to the Löwner order while the second one is to discuss the eigen (or singular) value inequalities and their variants.
In the direction of matrix inequalities a serious obstacle is in that
for ![]() the product AB is Hermitian (and positive semi-definite) only if
A
and B are commutative. If A and B are commutative,
through simultaneous diagonalization, the situations are almost the same
as the scalar case.
the product AB is Hermitian (and positive semi-definite) only if
A
and B are commutative. If A and B are commutative,
through simultaneous diagonalization, the situations are almost the same
as the scalar case.
There are several natural ways of defining a positive definite geometric mean for (non-commuting) positive definite A, B > 0. One candidate is
It is rather surprising to see that with this definition the arithmetic-geometric mean inequality is not valid in general. The only valid inequality is
The other candidate, denoted by ![]() ,
is
,
is
for which the arithmetic-geometric mean inequality is valid. This geometric
mean![]() admits several nice characterizations. First
admits several nice characterizations. First ![]() is proved to be the maximum of
is proved to be the maximum of ![]() for which
for which
![\begin{displaymath}\left[\begin{array}{cc} A & X \\ X & B \end{array}\right] \; \geq \;0.\end{displaymath}](img13.gif)
This implies that ![]() is a unique positive definite solution of the matrix quadratic equation
is a unique positive definite solution of the matrix quadratic equation ![]() It
is seen from this that despite its asymmetric appearance
It
is seen from this that despite its asymmetric appearance ![]() coincides with
coincides with ![]() .
.
There are many evidences which support rightness of this definition
of geometric mean. ![]() becomes the midpoint of a geodesic curve connecting A and B
with respect to a natural Riemannian metric on the cone of positive definite
matrices. Also there is an iteration scheme leading to this geometric mean
becomes the midpoint of a geodesic curve connecting A and B
with respect to a natural Riemannian metric on the cone of positive definite
matrices. Also there is an iteration scheme leading to this geometric mean ![]() using the arithmetic means and the harmonic means. Starting from
using the arithmetic means and the harmonic means. Starting from ![]() and
and ![]() ,
define
,
define
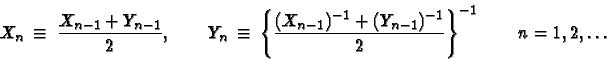
Then it is proved that both Xn and Yn
converge to ![]() .
In the same spirit a possible matrix generalization of atb1-t
may be
.
In the same spirit a possible matrix generalization of atb1-t
may be
for which the Young inequality is valid.
Let us turn to the eigen (or singular) value inequalities. For matrices
X,
Y
the singular value inequalities ![]() where
the singular values are arranged in non-increasing order, is equivalent
to the existence of a unitary matrix U such that
where
the singular values are arranged in non-increasing order, is equivalent
to the existence of a unitary matrix U such that ![]() .
In this connection the Schwarz inequality or more generally the Young inequality
is valid in the following form ; for general matrices X, Y
and for
.
In this connection the Schwarz inequality or more generally the Young inequality
is valid in the following form ; for general matrices X, Y
and for ![]() with 1/p + 1/q = 1 there
is a unitary matrix Usuch that
with 1/p + 1/q = 1 there
is a unitary matrix Usuch that
A weaker comparison is based on (weak) majorization relation among singular values, defined as
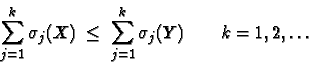
This is equivalent to the existence of a finite number of unitary matrices ![]() and a finite number of non-negative numbers
and a finite number of non-negative numbers ![]() with
with ![]() such that
such that
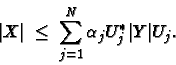
It is, however, more convenient to formulate this condition as ![]() for all unitarily invariant norms
for all unitarily invariant norms ![]() .
There is the Young inequality of the form; for
.
There is the Young inequality of the form; for ![]() and
for general matrix X
and
for general matrix X
Up to this point, for both matrix and singular value inequalities, the
most basic fact is that we are treating a pair of matrices. We shall
discuss, when ![]() ,
what is a reasonable definition of geometric mean of
,
what is a reasonable definition of geometric mean of ![]() and what kind of arithmetic-geometric mean inequalities are expected.
and what kind of arithmetic-geometric mean inequalities are expected.
Fisher's lack of fit test was based on having exact replicates in the
rows of the model matrix of a linear model. In recent years, considerable
work has been done on using clusters of near replicates to test for lack
of fit. If, instead of restricting ourselves to using clusters of near
replicates, we more generally create rational subgroups of the data in
which there is reason to believe that observations in a subgroup are more
similar than observations in different subgroups, the tests used for detecting
lack of fit have been shown to be sensitive to lack of independence. The
original motivation for this application was the observation that Shewhart's
means charts based on rational subgroups are sensitive, not only to nonconstant
mean values, but also are senstivie to lack of independence. To develop
graphical procedures for checking lack of independence (as well as lack
of fit) we returned to the idea of creating means charts. An obvious, but
naive and little referenced, method for creating means charts for linear
models is simply to create rational subgroups, average the residuals within
the rational subgroups, and chart these means of residuals. We discuss
the weaknesses of this naive approach, suggest two alternatives, examine
some theory for the alternatives, and explore the usefulness of all three
approaches.
Survo is a general environment for statistical computing and related areas (Mustonen 1992). Its current version SURVO 98 works on standard PC's and it can be used in Windows, for example. The first versions of Survo were created already in 1960's. The current version is based on principles introduced in 1979 (Mustonen 1980, 1982).
According to these principles, all tasks in Survo are handled by a general text editor. Thus the user types text and numbers in an edit field which is a rectangular working area always partially visible in a window on the computer screen. Information from other sources - like arrays of numbers or textual paragraphs - can also be transported to the edit field.
Although edit fields can be very large giving space for big matrices and data sets, it is typical that such items are kept as separate objects in their own files in compressed form and they are referred to by their names from the edit field. Data and text are processed by activating various commands which may be typed on any line in the edit field. The results of these commands appear in selected places in the edit field and/or in output files. Each piece of results can be modified and used as input for new commands and operations.
This interplay between the user and the computer is called `working in editorial mode'. Since everything is directly based on text processing, it is easy to create work schemes with plenty of descriptions and comments within commands, data, and results. When used properly, Survo automatically makes a readable document about everything which is done in one particular edit field or in a set of edit fields. Edit fields can be easily saved and recalled for subsequent processing.
Survo provides also tools for making new application programs. Tutorial mode permits recording of Survo sessions as sucros (Survo macros). A special sucro language for writing sucros for teaching and expert applications is available. For example, it is possible to pack a lengthy series of matrix and statistical operations with explanatory texts in one sucro. Thus stories about how to make statistical analysis consisting of several steps can be easily told by this technique. Similarly application programs about various topics are created rapidly as sucros.
Matrix computations are carried out by the matrix interpreter of Survo (originated in its current form in 1984 and continuously extended since then). Each matrix is stored in its own matrix file and matrices are referred to by their file names. A matrix in Survo is an object having the following attributes:
gives the vector of regression coefficients as a column vector (matrix file) B with internal name INV(X'*X)*X'*Y and with row labels which identify regressors and a (single) column label which is the name of the regressand. All statistical operations of Survo related e.g. to linear models and multivariate analysis give their results both in legible form in the edit field and as matrix files with predetermined names. Then it is possible to continue calculations from these matrices by means of the matrix interpreter and form additional results. When teaching statistical methods it is illuminating to use the matrix interpreter for displaying various details step by step.
The website of Survo (www.helsinki.fi/survo/eindex.html) will also contain
more information about the topic of this talk.
References
Mustonen, S. (1980). SURVO 76 Editor, a new tool for interactive statistical computing, text and data management. Research Report No. 19, Dept. of Statistics, University of Helsinki.
Mustonen, S. (1982). Statistical computing based on text editing. Proceedings in Computational Statistics, 353-358, Physica-Verlag, Wien.
Mustonen, S. (1992). Survo - An Integrated Environment
for Statistical Computing and Related Areas. Survo Systems, Helsinki.
For mixture models on the simplex, we discuss the improvement of a given
design in terms of increasing symmetry, as well as obtaining a larger moment
matrix under the Loewner ordering. The two criteria together define the
Kiefer design ordering. The Kiefer ordering can be discussed in the usual
Scheffé model algebra, or in the alternative Kronecker product algebra.
We employ the Kronecker algebra which better reflects the symmetries of
the simplex experiment region. For the second-degree mixture model, we
show that the set of weighted centroid designs constitutes a convex complete
class for the Kiefer ordering. For four ingredients, the class is minimal
complete. Of essential importance for the derivation is a certain moment
polytope, which is discussed in detail. Kiefer ordering of simplex designs
for second-degree mixture models with four or more ingredients.
* Joint work with Norman R. DRAPER
(University of Wisconsin, Madison, USA) and Berthold HEILIGERS
(Otto-von-Güricke-University, Magdeburg, Germany).
Suppose that ![]() is a log-likelihood function, where
is a log-likelihood function, where ![]() is the
is the ![]() vector of parameters of interest and
vector of parameters of interest and ![]() is a
is a![]() vector of nuisance parameters. Set
vector of nuisance parameters. Set ![]() .
We let
.
We let 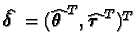 denote the maximum likelihood estimator of
denote the maximum likelihood estimator of ![]() and write the observed information matrix,
and write the observed information matrix, ![]() in
the partitioned form
in
the partitioned form
| = | ![$\displaystyle \left[\begin{array}{cc}-\frac{\partial^2\ell}{\partial\mbox{\bol......ial\mbox{\boldmath$\tau$ }\partial\mbox{\boldmath$\tau$ }^T}\end{array}\right]$](img45.gif) |
||
| = | ![$\displaystyle \left[\begin{array}{cc} {\mbox{\boldmath$\cal I$ }}_{\theta\theta......I$ }}_{\tau\theta} & {\mbox{\boldmath$\cal I$ }}_{\tau\tau} \end{array}\right].$](img46.gif) |
(1) |
The profile likelihood, ![]() ,
is defined by setting
,
is defined by setting ![]() .
Richards (1961) showed that, under suitable regularity conditions:
.
Richards (1961) showed that, under suitable regularity conditions:
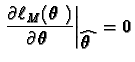 ;
and
;
and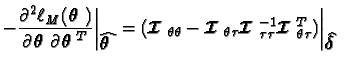 .
.![$\displaystyle\left[-\frac{\partial^2\ell_M({\theta})}{\partial\mbox{\boldmath$\......}\right]^{-1}_{\mbox{\boldmath$\theta$ }=\widehat{\mbox{\boldmath$\theta$ }}}$](img53.gif) is the asymptotic covariance matrix of
is the asymptotic covariance matrix of In this paper we use an extended version of Richards' result to produce
semi-parametric maximum-likelihood estimators of regression parameters
for a wide class of study designs and data structures in which some units
are not fully observed. (Case-control studies are the most common examples
of such studies; see Scott and Wild (1999) for a more complete list of
examples.) The nuisance ``parameter" here is the joint distribution function
of the covariates, something that is rarely of interest in its own right
and which is often impossible (or at least very difficult) to model.
References
Richards, F. S. G. (1961). A method of maximum likelihood estimation. J. Roy. Statist. Soc. B 23, 469-476.
Scott, A. J. and Wild, C. J. (1999). Semi-parametric maximum
likelihood inference for generalized case-control studies. J. Statist.
Plann. Inf. 69, in press.
* Joint work with Chris WILD
(University of Auckland, New Zealand).
An attempt is made at tracing the history of the use of matrices and
their algebra in statistics. Much of that history is quite recent, compared
to the age of matrices themselves. They are said to have originated in
1858; but barely entered statistics until the 1930s. Even the 1950s, when
multiple regression (a topic ideally and easily suited to matrix notation)
was coming to be widely taught and written about, that was mostly without
the use of matrices.
In this talk we address the problem of nonnegative estimation of variance
components in unbalanced multivariate mixed models with two variance components.
This generalizes the work in Mathew/Niyogi/Sinha (JMA, 1994). We also discuss
REML estimation of two variance components in univariate unbalanced models.
We illustrate our results with an example.
We revisit the elegant matrix equality first established in 1955 by the distinguished Chinerse mathematician Loo-Keng Hua (1910-1985):
Here both A and B are ![]() complex matrices, I is the identity matrix (In
is the
complex matrices, I is the identity matrix (In
is the ![]() identity matrix), * denotes conjugate transpose, and all the
singular values of A are strictly less than 1.
identity matrix), * denotes conjugate transpose, and all the
singular values of A are strictly less than 1.
We begin our paper by presenting Hua's original proof, which does not appear to be widely known [``Inequalities involving determinants" (in Chinese), Acta Math. Sinica 5 (1955), 463-470; English translation: Transl. Amer. Math. Soc. Ser. II 32 (1963), 265-272].
We then offer two new proofs, with some extensions, of Hua's matrix equality, and associated matrix and determinant inequalities. Our new proofs use a result concerning Schur complements, and an apparently new generalization of Sylvester's law of inertia. Each proof is useful in its own right, and we believe that these two proofs are new.
We continue by generalizing Hua's matrix equality and inequality, and
provide an upper bound as strong as the lower bound in Hua's determinantal
inequality. Some historical, biographical and bibliographic information
is also included.
* Joint work with Christopher C. PAIGE
(McGill University, Montréal, Canada), Bo-Ying WANG
(Beijing Normal University, Beijing, China) and Fuzhen ZHANG
(Nova Southeastern University, Fort Lauderdale, USA).
CONTRIBUTED PAPERS
The problem of estimation of characteristic roots of the covariance matrix of the multivariate normal distribution is considered. Stein-type and pretest estimators are proposed for the population characteristic root vector.
The statistical objective here is to investigate the merits of the proposed
estimators relative to the sample characteristic roots. It is demonstrated
that the proposed estimators are asymptotically superior to the sample
characteristic roots.
In the presence of collinearity certain biased estimation procedures
like ridge regression, generalized inverse estimator, principal component
regression, Liu estimator, or improved ridge and Liu estimators are used
to improve the ordinary least squares estimates in the linear regression
model. In this paper new biased estimator (Liu estimator), almost unbiased
(improved) Liu estimator and their residuals will be analyzed and compared
with OLS residuals in terms of mean squared error.
The present poster aims to give a brief explanation of my research in spatial statistics.
The study of composite materials have been increased in recent years. Studies about their composition and manufacture are extremely relevant for obtaining good results.
These materials consist of a solid matrix where several particles of other substances were embedded. It is of great importance to know the way these particles are distributed inside the material as this is going to influence the materials' quality and strength. Most composite materials are also opaque which makes it difficult to observe the particles distribution. The only possible way is to make a cut and observe the pattern obtained by the particles that were intercepted by that plane. This process is based on the application of several statistical tests. I intend to give an introduction about the tests used: Nearest Neighbour, F, J and Ripley's K functions and also their implementation on both spaces.
The main aim of this research is to try to infer (using spatial statistical
methods) the way particles are distributed in a three dimensional space
when only information from two dimensional spaces obtained from the same
material are available.
The methods of the written, telephone and personal questionings have been established for many years. Here the method of Direct Mailing is introduced.
The method of Direct Mailing means that a letter of transmittal was sent by means of e-mail, which refers to a questionnaire, which is at the WWW. Therefore representativity is ensured. Further the structure of the questionnaire can be carried out by the usual method of the written questionnaire.
The investigation was limited to students of Graz University of Technology, Austria.
On Friday, 9 October 1998 at 16:45 an e-mail was coincidentally sent to 1000 students in which they were asked to click and fill out the questionnaire on the network.
The date Friday, 9 October 1998 (16:45) was selected because:
The questionnaire consists 27 questions about the internet and also
5 demographic questions. Our response rate was situated after 4 days when
the e-mail was sent of approximately 25 per cent, i.e. 75 per cent of all
responses, this increased after termination of the empirical study to approximately
34 per cent. On Monday, 12 October 1998 we received 123 responses, which
corresponds to a response rate of approximately 13 per cent on this day.
The overall distribution on the basis of the response arrival times was
left-skewed. Separated the distribution per weekdays and weekend days showed
that the response arrival times depended on them.
The method of quasi-least squares has been introduced and developed
recently in a series of three papers: Chaganty (1997), Shults and Chaganty
(1998), and Chaganty and Shults (1999). These papers are concerned with
estimating the parameters in longitudinal data analysis problems that occur
in the framework of generalized linear models. In this talk I will discuss
the application of the method to analyze growth curve models and some multivariate
discrete models. I will also discuss some test statistics and their large
sample properties. Finally, examples will be given to illustrate the method
on real life data.
The special manifolds of our interest in this paper are the Stiefel
manifold and the Grassmann manifold. Formally, the Stiefel manifold
Vk,m
is the space of k-frames in the m-dimensional real Euclidean
space Rm, represented by the set of ![]() matrices X such that X'X=Ik,
where Ik is the
matrices X such that X'X=Ik,
where Ik is the ![]() identity matrix, and the Grassmann manifold Gk,m-k
is the space of k-planes (k-dimensional hyperplanes) in Rm.
We see that the manifold Pk,m-k
of
identity matrix, and the Grassmann manifold Gk,m-k
is the space of k-planes (k-dimensional hyperplanes) in Rm.
We see that the manifold Pk,m-k
of ![]() orthogonal projection matrices idempotent of rank k corresponds
uniquely to Gk,m-k. This paper
is concerned with statistical analysis on the manifolds Vk,m
and Pk,m-k as statistical sample
spaces consisting of matrices. For the special case k=1, the observations
from
V1,m and G1,m-1
are regarded as directed vectors on a unit sphere and as axes or lines
undirected, respectively. There exists a large literature of applications
of directional statistics and its statistical analysis, mostly occurring
for m=2 or 3 in practice, in Geological Sciences, Astrophysics,
Biology, Meteorology, Medicine and other fields. The analysis of data on
the general Stiefel manifold Vk,m is
required especially for
orthogonal projection matrices idempotent of rank k corresponds
uniquely to Gk,m-k. This paper
is concerned with statistical analysis on the manifolds Vk,m
and Pk,m-k as statistical sample
spaces consisting of matrices. For the special case k=1, the observations
from
V1,m and G1,m-1
are regarded as directed vectors on a unit sphere and as axes or lines
undirected, respectively. There exists a large literature of applications
of directional statistics and its statistical analysis, mostly occurring
for m=2 or 3 in practice, in Geological Sciences, Astrophysics,
Biology, Meteorology, Medicine and other fields. The analysis of data on
the general Stiefel manifold Vk,m is
required especially for ![]() in practical applications, and the Grassmann manifold is a rather new subject
treated as a statistical sample space.
in practical applications, and the Grassmann manifold is a rather new subject
treated as a statistical sample space.
Among population distributions uniform and non-uniform defined on the
special manifolds, the matrix Langevin distributions are most commonly
used for statistical analyses. The matrix Langevin distributions are exponential
whose density functions are proportional to ![]() .
The problems of estimation and tests for hypotheses of the parameters and
of classifications of the matrix Langevin distributions and the related
sampling distributions are expressed in terms of hypergeometric functions
with matrix arguments. The solutions for these inference and distribution
problems can be asymptotically evaluated for large sample size, for large
concentration, or for high dimension.
.
The problems of estimation and tests for hypotheses of the parameters and
of classifications of the matrix Langevin distributions and the related
sampling distributions are expressed in terms of hypergeometric functions
with matrix arguments. The solutions for these inference and distribution
problems can be asymptotically evaluated for large sample size, for large
concentration, or for high dimension.
By applying Procrustes methods we are led to the concept of Procrustes distance defined on the special manifolds as well as the usual Euclidean one. These distance measures are useful in constructing suitable (kernel) density estimators in the theory of density estimation and in defining measures of association on the manifolds. Statistical problems on the special manifolds are transformed to those on the Euclidean spaces by using the decomposition theorems of the manifolds; e.g., in evaluating multiple integrals and generating new population distributions on the manifolds.
A detail discussion will be given of those problems raised above which
are of unique character as statistical analyses on our special manifolds.
In this paper, we derive some simple formulae to express the correlation
coefficient between two random variables in the case of a linear relationship.
One of these representations, the cube of the correlation coefficient,
is given as the ratio of the skewness of the response variable to that
of the explanatory variable. This result, along with other expressions
of the correlation coefficient presented in this paper, has implications
for choosing the response variable in a linear regression modelling.
Keywords: Correlation, least squares, linear regression,
response variable, direction dependence regression, skewness.
This paper deals with an approach due to Christian Grillenberger, late professor of mathematical stochastics at the University of Kassel, Germany. He passed away of a heart attack at the 25th of May, 1998.
The problem of jointly diagonalizing complex ![]() -matrices
was dealt in many papers. The necessary and sufficient condition is that
the involved matrices commute. Grillenberger gave a easy proof that also
the projections appearing in the spectral decompositions commute. This
results in simple simultaneous decompositions.
-matrices
was dealt in many papers. The necessary and sufficient condition is that
the involved matrices commute. Grillenberger gave a easy proof that also
the projections appearing in the spectral decompositions commute. This
results in simple simultaneous decompositions.
If A and B are rectangular matrices the hermiticity of
both AB and BA is the necessary and sufficient condition
for a joint singular decomposition. It is shown that this can also be obtained
from Grillenberger's result. Generalizations to a finite number of matrices
are obvious.
Three distinct variants of the method of averages were proposed by Tobias
Mayer in 1750, by Pierre Simon Laplace in 1788, and by Pierre Simon Laplace
again in 1818. Even though the merits of the method of least squares became
apparent in the 1820s and 1830s, these and other variants of the method
of averages has continued to be employed by leading practical scientists
until relatively recent times. In this paper, we outline some of the optimality
results that have been established in respect of this fitting procedure.
In applied experimental design studies and in the theoretical studies of linear models the efficiency and the unbiasedness of the estimates have been considered but the studies have followed different paths. This study is an attempt to bridge the gap between these two research traditions.
If there are regressors of minor interest then a central problem is if the corresponding nuisance parameters should be included in the linear model or not. If the true model contains the nuisance parameters but we ignore them when estimate the main parameters then usually the estimates are biased. On the other hand if the nuisance parameters can be left out but we include them in the model then the estimates of the main parameters may be inefficient.
In applied research the interest has mainly been concentrated on the effect of these model mis-specifications on the estimates of the individual parameters. However, there may be parametric functionals which are robust against these mis-specifications. Within a more general framework Nordström and Fellman (LAA 127, 341-361) have discussed these problems. If the reduced model and the large model are nested then the subset of parametric functionals, which are ``bias-robust" with respect to underspecification, is equal with the subset of parametric functionals, which are ``variance-robust" with respect to overspecification. The coefficient vectors of such functionals belong to the orthogonal complement of the range of the alias (bias) matrix. If the inclusion or exclusion of block effects are considered then the models are not nested but using Khuri's generalized orthogonal block condition similar results can be obtained.
We present some theoretical results and elucidate them with examples
from the literature. In this study we mainly consider bias-robustness of
the estimates.
The main problem considered in the paper is studing properties of maximum
likelihood estimators MLE's in certain mixed models with two variance components.
It is shown how much MLE's can be biased. Some propositions is given how
to improve them to make the biasedness smaller. Two way layouts models
are considered in details, for which results of simulations are presented.
A formula for the Moore-Penrose inverse of an arbitrary partitioned
symmetric nonnegative definite matrix is derived, and some necessary and
sufficient conditions for the coincidence of our formula with the so called
generalized Banachiewicz formula are given. Eventually, a Löwner ordering
relationship between a generalized Schur complement in the matrix and a
generalized Schur complement in it's Moore-Penrose inverse is revealed.
Let A and B be nonnegative definite matrices. It is known
that the Löwner partial ordering ![]() implies
implies ![]() only for some classes of functions [see Löwner (1934)] and it is true
in the case of
only for some classes of functions [see Löwner (1934)] and it is true
in the case of ![]() not for all matrices [see Stepniak (1987)], but is true for commuting matrices.
Mathias (1991) analysed conditions for the equivalence of the above inequalities.
We are interested in the implication:
not for all matrices [see Stepniak (1987)], but is true for commuting matrices.
Mathias (1991) analysed conditions for the equivalence of the above inequalities.
We are interested in the implication: ![]() implies
implies ![]() .
The aim is to characterize matrices C and scalars c for which
the implication is true. Taking matrix C as an identity matrix we
obtain special case of inequalities analysed by Nordström and Mathew
(1996). Some statistical applications of the inequalities are pointed out.
.
The aim is to characterize matrices C and scalars c for which
the implication is true. Taking matrix C as an identity matrix we
obtain special case of inequalities analysed by Nordström and Mathew
(1996). Some statistical applications of the inequalities are pointed out.
References
Löwner, K. (1934). Über monotone Matrixfunktionen. Math. Z. 38, 177-216.
Mathias, R. (1991). The equivalence of two partial orders on a convex cone of positive semidefinite matrices. Linear Algebra Appl. 151, 27-55.
Nordstrom, K. and Mathew, T. (1996). Inequalities for sums of matrix quadratic forms. Linear Algebra Appl. 237/238, 429-447.
Stepniak, C. (1987). Two orderings on a convex cone of
nonnegative definite matrices. Linear Algebra Appl. 94, 263-272.
When reliable population data are available from the vital registration
system, they are eventually sufficient to be used for analysing the demographic
characteristics of the country and their important related implications.
In fact, the reliability of the vital registration data in developing countries
as well as some communities in developed countries (indigenous communities
for example) is seriously affected by the problems of under-registration
and age misreporting. Although the problem of misreporting of population
data in developed countries has been tackled through many studies in literature
(Keyfitz 1984, Ishak 1987 and Sivamurthy 1989), the more influential problem
of under-registration is still a real obstacle towards a more valid estimates
for population figures in these countries. Mortality data, especially of
the childhood span, are known to be the mostly affected data by under registration.
In fact, between one-third and two-third of the infant deaths in developing
countries are escaping registration (International Institute of Statistics
1987). In this paper, some mathematical and regression techniques were
presented to model the under registration behaviour, where only limited
information about the magnitude of the problem in the country is available.
The derived model was then combined with a regression model for infant
mortality to finally present an improved model that is free from the effects
of both the under registration and age misreporting problems. To verify
the applicability of the model, this was applied to the infant mortality
data of Egypt. The model could reflect an acceptable pattern of infant
mortality in the country which is significantly higher in reliability than
the pattern reflected by the officially published data.
Keywords: Direct/Indirect survival estimation,
demographic estimations from incomplete data, mortality models, under registration
model.
Alpha designs are a class of resolvable incomplete block designs and
are widely used in practice, particularly in plant and tree breeding trials.
An alpha design for r replicates and block size k can be
generated from a ![]() array of numbers modulo s, where v=sk is the number
of treatments in the design. Alpha designs are available for a wide range
of parameter combinations. For some of these combinations they correspond
to the well-known square and rectangular lattice designs and hence are
optimal, i.e. they have maximum average efficiency factor, E. In
general, however, computer search methods are used to choose the best alpha
design, i.e. the design with E closest to a known theoretical upper
bound. The calculation of E involves matrix inversions and so more
easily obtained objective functions are used in the search algorithms.
Typical surrogate objective functions include the trace of the square and
cube of the design information matrix. There is, however, the danger that
such alternatives can lengthen the computer search and perhaps even prevent
the optimal design being found. This is particularly the case for computer
search procedures based on exchange and interchange algorithms, e.g. the
design generation package CycDesigN carries out random interchanges on
the alpha array.
array of numbers modulo s, where v=sk is the number
of treatments in the design. Alpha designs are available for a wide range
of parameter combinations. For some of these combinations they correspond
to the well-known square and rectangular lattice designs and hence are
optimal, i.e. they have maximum average efficiency factor, E. In
general, however, computer search methods are used to choose the best alpha
design, i.e. the design with E closest to a known theoretical upper
bound. The calculation of E involves matrix inversions and so more
easily obtained objective functions are used in the search algorithms.
Typical surrogate objective functions include the trace of the square and
cube of the design information matrix. There is, however, the danger that
such alternatives can lengthen the computer search and perhaps even prevent
the optimal design being found. This is particularly the case for computer
search procedures based on exchange and interchange algorithms, e.g. the
design generation package CycDesigN carries out random interchanges on
the alpha array.
This talk presents a recursive method that allows an efficient updating
procedure for E as part of the exchange algorithm operating on the
alpha array. The method leads to some interesting results involving Hermitian
matrices. The new updating procedure for E compares very favourably
with the existing approaches based on surrogate objective functions and
not only speeds up the search for near-optimal alpha designs, but often
results in the generation of designs with improved E. Some comparisons
will be presented.
Consider a vector valued response variable related to a vector valued
explanatory variable through a normal multivariate linear model. The multivariate
calibration deals with statistical inference on unknown values of the expanatory
variable. The problem addressed is the construction of joint confidence
regions for several unknown values of the explanatory variable. The problem
is investigated when the variance covariance matrix is a scalar multiple
of the identity matrix and also when it is a completely unknown positive
definite matrix. An exact confidence region is constructed by generalizing
the results in Mathew and Kasala (1994, The Annals of Statistics).
In a pioneering paper (1953) Whittle developed a formula for expressing
Fisher's information matrix of multivariate time series models. It is described
in function of the spectral density of the time series process. The existing
relationship is extended to the whole matrix instead of one element and
is related with an alternative expression. The Hermitian property of the
matrices under study allows us to formulate the link in a theorem which
is further illustrated with an example.
Keywords: Spectral density, Hermitian matrix, permutation
matrix.
The most commonly used methods for approximating density and distribution
functions are Edgeworth type expansions. Usually it is assumed that the
dimension of the approximating distribution is the same as the dimension
of the distribution which has to be approximated. In this paper we are
going to examine multivariate expansions where the dimensions of the distributions
can be different. In many situations it seems natural to approximate some
multivariate distribution with a distribution of higher dimensionality.
The sample correlation matrix R as a function of the sample covariance
matrix S represents a typical example of the case: one might be
interested in approximating the joint distribution of ![]() nonsymmetric random elements of R with the joint distribution of
nonsymmetric random elements of R with the joint distribution of ![]() different random elements of S.
different random elements of S.
In Kollo & von Rosen (1998) a general formula is obtained to represent a multivariate density through another (possibly higher-dimensional) density as a formal series expansion where derivatives of the approximating density and cumulants of both random vectors (matrices) appear in growing orders in the terms of the expansion.
This general result was applied for approximating of the density of the sample correlation matrix R. The first terms of the expansion include the cumulants of R up to the third order. Approximate expressions of the cumulants have been found in the paper using an expansion of the characteristic function of R. Later the cumulants were used in the density approximation formulae, based on Wishart distribution and multivariate normal distributions.
In the twodimensional case a simulation experiment was carried out i.e.
the density of the sample correlation coefficient was approximated by the
Wishart distribution and the multivariate normal distribution. These approximations
were compared with the simulated empirical distributions and the classical
univariate Edgeworth expansion.
Reference
Kollo, T. and von Rosen, D. (1998). A unified approach
to the approximation of multivariate densities. Scandinavian Journal
of Statistics, 25, 93-109.
Given a square matrix A, the maximum distance between its eigenvalues
is known as spread of A. A new characterization for the spread of
a normal matrix is presented. New bounds for the spread have been obtained
and compared. Some of our results are generalizations of known results.
These bounds have application in Statistics.
Analysis methods for longitudinal or clustered categorical data are currently a hot reserarch topic. Most of these rely on asymptotic theory for the justification of inferences. To assess the small-sample behaviour of these methods, we need to be able to generate random vectors having a variety of categorical distributions. A feature of several of these generation methods is the use of the inversion algorithm, which requires that the joint distribution of the correlated variates be completely specified.
Suppose we have a random n-vector of categorical variates, ![]() ,
Yn),
where Yi may assume any one of the values
,
Yn),
where Yi may assume any one of the values ![]() ,
and let
,
and let ![]()
![]() be its joint probability function. In many cases the probabilities
be its joint probability function. In many cases the probabilities ![]() may be quite difficult to specify analytically, but simple formulae may
exist for the cumulative probabilities
may be quite difficult to specify analytically, but simple formulae may
exist for the cumulative probabilities
In this talk we describe develop a simple, general recursive method
of calculating the p's from the P's which is based on Kronecker
products. If p and P are the N-vectors whose elements
are ![]() and
and ![]() ,
arranged in lexicographic order, then
,
arranged in lexicographic order, then
| (1) |
where ![]() denotes the Kronecker product, and Ak is the
denotes the Kronecker product, and Ak is the ![]() matrix
with ones on and below the diagonal, and zeroes above. To compute p
from P, we invert (1) and get
matrix
with ones on and below the diagonal, and zeroes above. To compute p
from P, we invert (1) and get
| (2) |
The matrix inverse of Ak can be given explicitly: it is
![\begin{displaymath}A_k^{-1}=\left[\begin{array}{cccccc}1&0&0&\cdots&0&0\\-1......&\ddots&\vdots&\vdots\\0&0&0&\cdots&-1&1\end{array}\right ].\end{displaymath}](img79.gif)
We describe a recursive S function to implement the method and give
several examples.
We consider a general multivariate conditional heteroskedastic time
series model and derive a representation for the information matrix of
the maximum likelihood estimator by using the standard matrix differential
calculus techniques. As a special case, we discuss the VAR-VARCH model,
and demonstrate the maximum likelihood estimation of the information matrix
in an example with simulated data.
Admissible and linearly sufficient estimators in restricted linear model
are considered. These estimators are found in Heiligers and Markiewicz
(1996) to be special general ridge estimators. A preliminary study of their
robustness (validity) was made in Markiewicz (1998) in the context of the
correct model and the assumed model, resulting in specification errors.
Robustness properties of the estimators are studied regarding misspecification
of the dispersion matrix of the errors vector, the model matrix, and parameters
restrictions. Some robust estimators are characterized.
Keywords: Admissibility, linear sufficiency, general
ridge estimator, restricted linear model.
AMS Subject Classification: Primary 62F10; secondary
62J05.
References
Heiligers, B. and Markiewicz, A. (1996). Linear sufficiency and admissibility in restricted linear models. Statist. Probab. Lett. 30, 105-111.
Markiewicz, A. (1998). Comparison of linear restricted
models with respect to the validity of admissible and linearly sufficient
estimators. Statist. Probab. Lett. 38, 347-354.
In this paper we present some results concerning canonical correlations
in two- and three-way layouts. A useful proposition relating the canonical
correlations to the singular values of a specific matrix is proved and
a geometrical explanation is given. Furthermore, some formulas concerning
the numbers of unit canonical correlations in a three-way layout are given
and even they are generalized for k-way layout.
In the talk, we shall describe the construction of tolerance regions
and simultaneous tolerance regions in a multivariate linear regression
model. Of particular interest will be the problem of obtaining suitable
approximations to the tolerance factor. Following the ideas given by John
(Sankhya, 1963), we shall consider several approximate tolerance
factors and report the accuracy of the approximations, numerically. The
numerical computation of the simultaneous tolerance factor wil be explained
and the results will be illustrated using an example.
Let A be a nonnegative ![]() matrix with row sums r1, r2,
matrix with row sums r1, r2, ![]() ,
rn
and Perron root
,
rn
and Perron root ![]() .
It is well-known that
.
It is well-known that ![]() ,
where the minimum and the maximum are taken over all the i's with
ri
> 0. Using a simple shifting technique, we find bounds for
,
where the minimum and the maximum are taken over all the i's with
ri
> 0. Using a simple shifting technique, we find bounds for ![]() ,
which appear to be amazingly good in general. We also study the behaviour
of these bounds applied to powers of A.
,
which appear to be amazingly good in general. We also study the behaviour
of these bounds applied to powers of A.
This talk considers some difficulties - inspired by Belsley (1991) -
related to interpretation of the relation between the correlation and corresponding
cosine. We illustrate how carefully we must take steps in the world of
collinearity. Numerical calculations are done using Survo - a statistical
software developed by Professor Seppo Mustonen; for general features of
Survo, see Mustonen (1992, 1999).
References
Belsley, David A. (1991). Conditioning Diagnostics: Collinearity and Weak Data in Regression. Wiley, New York.
Mustonen, Seppo (1992). Survo: An Integrated Environment for Statistical Computing and Related Areas. Survo Systems, Helsinki.
Mustonen, Seppo (1999). Matrix computations in Survo.
Abstracts
of the Eighth International Workshop on Matrices and Statistics. Dept.
of Mathematics, Statistics & Philosophy, University of Tampere, Finland.
Any linear experiment can be presented as an information channel transforming
a signal ![]() into the observation vector
into the observation vector ![]() .
Suppose that X is transformed again in this way and results in a
new random vector Y. It seems natural that the initial vector X
is at least as informative as Y. It would be interesting to converse
the problem.
.
Suppose that X is transformed again in this way and results in a
new random vector Y. It seems natural that the initial vector X
is at least as informative as Y. It would be interesting to converse
the problem.
Many orderings of statistical experiments or random vectors, considered
in the literature, include the phrase ``![]() is at least as informative as
is at least as informative as ![]() "
or ``
"
or ``![]() is at least as good as
is at least as good as ![]() ".
Which of the orderings can be presented as an information channel
".
Which of the orderings can be presented as an information channel![]() ?
?
Our aim is to answer this question.
A. Pattern of signs of first type is defined as a symmetric matrix S of order k having all elements equal to +1 or -1 and positive elements ones on the main diagonal. As it follows, the number m(k) of different patterns of signs of order k equals
Let ![]() be the set of all correlation matrices of order k. We are interested
in correlation matrices having given structure of signs and hence describing
some special dependence structure.
be the set of all correlation matrices of order k. We are interested
in correlation matrices having given structure of signs and hence describing
some special dependence structure.
Let S be a fixed pattern of signs and ![]() be a number from the interval
be a number from the interval ![]() .
Then the matrix
.
Then the matrix
| (1) |
consists of ones on main diagonal and all other elements equal either ![]() or
or ![]() .
Our question is - when is matrix R a correlation matrix?
.
Our question is - when is matrix R a correlation matrix?
More precisely, we are interested to find for each pattern of signsS
the set ![]() of values
of values ![]() in such a way that the following inclusion holds:
in such a way that the following inclusion holds:
It has been proved that the set ![]() is an interval
is an interval ![]() where the inequalities
where the inequalities
hold. The values ![]() and
and ![]() are limiting correlations for the pattern of signs S, and
the corresponding correlation matrices (1)
are extremal in the sense that they belong to the boundary set of
the set
are limiting correlations for the pattern of signs S, and
the corresponding correlation matrices (1)
are extremal in the sense that they belong to the boundary set of
the set ![]() .
.
The structure of the set ![]() (for given k) is determined by the set of different limiting correlations.
The extremal values -1 and +1 occur for very special patterns of signs
only.
(for given k) is determined by the set of different limiting correlations.
The extremal values -1 and +1 occur for very special patterns of signs
only.
B. Pattern of signs of the second type is a symmetric matrix Q of order k having all elements equal to +1, -1 or 0 and positive elements on the main diagonal. As it follows, the number n(k) of different patterns of signs of the second type of order k is much more compared with the number of patterns of signs of the first type and equals
The next problem is to find for each pattern of signs Q the set ![]() of values
of values ![]() in such a way that the following inclusion holds:
in such a way that the following inclusion holds:
In the report the results known for the patterns of signs of the first
type will be expanded for the patterns of signs of the second type, too.
The set of quaternions has been introduced by Sir William Rowan Hamilton
in 1843. By representing quaternions as 4-dimensional vectors and the multiplication
of quaternions as matrix-by-vector-product we provide a matrix oriented
approach to the topic. We will investigate properties of the fundamental
matrix and use the approach to derive basic and advanced properties of
the multiplication of quaternions. As an application of our approach we
will examine a quaternion equation which has been frequently considered
in the literature.
Data with missing values, some three-way data analysis models and some robust estimators of the correlation coefficients may induce correlation matrix A not positive definite (psd). In general, an approximation method for recovering the psd property should transform A (linearly or nonlinearly) into a correlation matrix R, according to a defined loss function, avoiding: (i) changes in the strict monotone relations among the correlation coefficients and (ii) opposite relations between the corresponding elements of the observed and the approximated correlation matrix. Neglecting (i) and (ii) generally induces the change in the ``true" correlation pattern of A and may lead to contradictory conclusions in the following multivariate analyses based on R instead of A.
In this paper monotone parametric and non-parametric constrained transformations
of the matrix A are introduced to find the least squares approximation
of A subject to constraints avoiding (i) and (ii).
A parametric analytical local minimum is determined as well as the optimal
solution obtained by solving quadratic constrained problems through optimization
tools. Some examples are examined to show the proposed transformations.
Keywords: Correlation, positive definite and positive
semi-definite matrices, numerical methods, least squares approximation.
Essential references
Browne, M. W. (1992). Circumplex models for correlation matrices. Psychometrika, 57, 4, 469-497.
Devlin, S., Gnanadesikan R. and Kettenring, J. R. (1975). Robust estimation and outlier detection with correlation coefficients. Biometrika, 62, 3, 531-545.
Giovagnoli A. and Romanazzi M. (1990). A group majorization ordering for correlation matrices. Linear Algebra and Its Applications, 127, 139-155.
Grone, R., Pierce S. and Watkins W. (1990). Extremal correlation matrices. Linear Algebra and Its Applications, 134, 63-70.
Knol, D. L. and ten Berge, J. M. F. (1989). Least-squares
approximation of an improper correlation matrix by a proper one. Psychometrika,
54, 1, 53-61.
This paper deals with the linear aggregation problem. For the
true
underlying micro relations, which explain the micro behaviour of the individuals,
no restrictive rank conditions are assumed. We compare several estimators
for the systematic part of the corresponding macro relations.
The main subject of the talk is Distance optimality criterion that was
put forward by B. Sinha (On the optimality of some designs, Calcutta
Stat. Assoc. Bull. 1970, 20, 1-20) quite long ago but has not
drawn much attention in the literature for the present. The essense of
this criterion within the framework of linear regression model ![]() ,
where y is a vector of observations having normal distribution,
,
where y is a vector of observations having normal distribution, ![]() is a vector of unknown regression parameters,
is a vector of unknown regression parameters, ![]() is a constant,
I is a unit matrix and X is a design matrix
of full rank, is the following. We would like to choose such a design that
is a constant,
I is a unit matrix and X is a design matrix
of full rank, is the following. We would like to choose such a design that
where ![]() is the usual least squares estimator of
is the usual least squares estimator of ![]() .
.
The close connection of Distance optimality criterion with the notion of stochastic domination turns out to be quite obvious. This connection allows to establish some useful properties of Distance criterion. We also introduce and discuss some new optimal design criterions based on other notions of stochastic majorization, which are weaker than stochastic domination.
Studying of Distance criterion via stochastic majorization has motivated
us to formulate some interesting design criterions more. Firstly, it is
worth noting that in the case of one unknown regression parameter, Distance
criterion is defined via the peakedness of the distribution of ![]() according to Birnbaum (On random variables with comparable peakedness,
Annals
of Mathematical Statistics, 1948, 19, 76-81). It is also well
known that Birnbaum's definition was generalized to the multivariate case
by Sherman (A theorem on convex sets with applications, Annals
of Mathematical Statistics, 1955,
26, 763-766). So, in the case
when
according to Birnbaum (On random variables with comparable peakedness,
Annals
of Mathematical Statistics, 1948, 19, 76-81). It is also well
known that Birnbaum's definition was generalized to the multivariate case
by Sherman (A theorem on convex sets with applications, Annals
of Mathematical Statistics, 1955,
26, 763-766). So, in the case
when ![]() is a vector, one can take Sherman's definition as a base for optimality
criterion, though this criterion turns out to be strong enough. Secondly,
it is easy to note that Distance criterion is defined via the Euclidean
error
is a vector, one can take Sherman's definition as a base for optimality
criterion, though this criterion turns out to be strong enough. Secondly,
it is easy to note that Distance criterion is defined via the Euclidean
error ![]() but one can take instead of that the generalized Euclidean error
but one can take instead of that the generalized Euclidean error ![]() as well for given symmetric positive definite matrix D.
as well for given symmetric positive definite matrix D.
We apply our considerations and solve optimal design problems mainly
for the case of one-way first degree polynomial fit model.
In the paper we deal with the usual mixed linear models. Thus the natural
parameter space make variance components and parameters corresponding to
the fixed effects. In this paper we present a relationship between quadratic
estimation and testing hypothesis for some linear functions of the model
parameters. In the problem of testing hypotheses for fixed parameters is
well known F-test which accepts null hypotheses if a ratio of the quadratic
lengthes of residuals under hypothesis and model is less than a given critical
value. In the paper Michalski and Zmyslony (1996) it is proposed a test
for vanishing of single variance component in more general linear model.
A null hypothesis is rejected if the ratio of the positive and negative
part of the locally best quadratic unbiased estimator of this component
is sufficiently large. In this paper it is proved that F-test can be derived
in the same way it means as a ratio of the positive and negative part of
a quadratic unbiased estimator for a corresponding quadratic function connected
with null hypothesis. Thus we get unified theorem for constructing tests
for hypotheses about both fixed effects and variance components. Testing
hypothesis for independence of binormal distribution will be presented
as an application of the result.
Keywords: Mixed linear models, variance components,
quadratic unbiased estimation, testing hypotheses, one-way classification
model.
AMS Subject Classification: 62F03, 62J10.
References
Gnot, S. and Michalski, A. (1994). Tests based on admissible estimators in two variance components models. Statistics, 25, 213-223.
Lehmann, E. L. (1959). Testing Statistical Hypotheses. Wiley, New York.
Michalski, A. and Zmyslony, R. (1996). Testing hypotheses for variance components in mixed linear models. Statistics, 27, 297-310.
Rao, C. R. (1973). Linear Statistical Inference and
its Applications, 2nd ed. Wiley, New York.
A random linear model for spatially located sensors measured intensity
of a source of signals in discrate instants of time is considered. A basis
of a quadratic subspace useful in quadratic estimation of a function of
model parameters is given.
PhD SESSION
Autocorrelated errors in regression models are responsible for biased estimation of the standard error of coefficient estimates. They also affect the type I error risk of classical F-test of the model and classical t-test of individual coefficients. Hence it is important to take into account the autocorrelated errors in the considered statistical test.
In this paper, we consider ten potential statistical procedures for valid hypothesis testing in regression models with autocorrelated errors. One of them is ordinary least-squares estimation. Three of them are based on generalized least-squares estimation of the slopes, combined with classical t-test. These procedures differ in the nature (constant or random) and the structure of the variance-covariance matrix used for generalized least-squares estimation; see Searle (1971), depending on whether the autocorrelation model and the parameter values are known, or not. Three other procedures are inspired from modified testing in repeated measures analysis of variance; see Greenhouse and Geisser (1959) and also Huynh and Feldt (1976). These three procedures differ in the nature and structure of the variance-covariance matrix used for modifying the number of degrees of the t-test, whereas parameters are estimated by ordinary least squares. The last three procedures considered here originate from modified t-test developed in correlation analysis; see Clifford et al. (1989) and Dutilleul (1993).
We investigate by simulation the type I error risk of all ten procedures
in the case of simple linear regression with time series data and an AR(1)
structure of the errors for positive and negative values of the autocorrelation
parameter. The design matrix can be of three types, fixed following a trend,
pseudo-random or random following a first order auto regressive process.
Results are discussed in terms of validity. A test procedure is said to
be valid if the probability of rejecting the null hypothesis when actually
the null hypothesis is true is less than or equal to some specified value,
say 0.05.
* Joint work with Pierre DUTILLEUL
(McGill University, Montréal, Canada).
In the report, we make a comparison of the orthogonal regression (OR) estimator and the least squares (LS) estimator of the parameters of the autoregressive system:
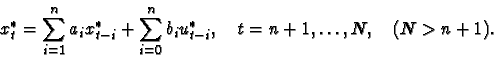
The both ``proper'' and ``non-proper'' disturbances are considered,
namely, those under which the estimators do not possess the estimate consistency,
asymptotic unbiasedness, etc. We prove the theorem about the LS and the
OR estimators identity as functions of data in the first order term of
the Taylor-series expansion with respect to the ``true'' non-perturbed
data value. Then, by Monte-Carlo analysis, we investigate the region of
the estimates' linear dependence on the data under small disturbances.
By the above theorem, in this region the LS and the OR estimators are identical.
To implement more thorough Monte-Carlo simulations, the terms up to third
order in the Taylor-series expansions for both the LS and the OR estimation
criteria were analytically achieved. It was found that under circumstances
considered as quite general, with non-proper disturbances, the OR estimator
yields less the mean square deviation, than the LS estimator.
We are interested in the following two theorems :
THEOREM 1.
Let the random vector x follow a multivariate
normal distribution with mean vector![]() and dispersion (variance-covariance) matrix V, not necessarily positive
definite. Let A and B be symmetric non-random matrices. Then x'Ax
and x'Bx are independently distributed if and only if
and dispersion (variance-covariance) matrix V, not necessarily positive
definite. Let A and B be symmetric non-random matrices. Then x'Ax
and x'Bx are independently distributed if and only if
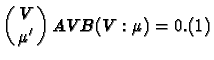
That (2b) implies (2a) is "obvious". We note that when V = I in (1) then it reduces to AB = 0, and so then x'Ax and x'Bx are independently distributed if and only if AB = 0.
Both Theorem 1 and Theorem 2 have been called the Craig-Sakamoto Theorem
(or Lemma). In this talk we review several "proofs" of Theorems 1 and 2
that have been presented in the literature and present a new proof of Theorem
2. We also present some biographical and historical information, as well
as an extensive bibliography.
* Joint work with S. W. DRURY
and George P. H. STYAN (both
of McGill University, Montréal, Canada). Part of an MSc thesis at
McGill University.
Consider the general linear mixed model ![]() where y is an n-dimensional normally distributed random vector with
where y is an n-dimensional normally distributed random vector with
X is a known ![]() matrix,
matrix, ![]() is an unknown p-dimensional vector of fixed parameters, Vi
, i=1,2,...,r, are known
nonnegative definite matrices while
is an unknown p-dimensional vector of fixed parameters, Vi
, i=1,2,...,r, are known
nonnegative definite matrices while ![]() is a vector of unknown variance components.
is a vector of unknown variance components.
For a given nonnegative definite ![]() matrix F and a given vector f=(f1,...,fr)'
with nonnegative components fi, I am interested in estimation
of the following nonnegative parametric function
matrix F and a given vector f=(f1,...,fr)'
with nonnegative components fi, I am interested in estimation
of the following nonnegative parametric function
by a quadratic estimator y'Ay, where the matrix Ais both symmetric and positive semidefinite.
For r=1 and V1=I, i.e. in the case of
the linear regression model, estimating of ![]() was investigated by Gnot, Trenkler and Zmyslony (1995) (J. Multivariate
Analysis 54). Applications to the problem of variable selection
in linear regression were presented in Gnot, Knautz and Trenkler (1994).
was investigated by Gnot, Trenkler and Zmyslony (1995) (J. Multivariate
Analysis 54). Applications to the problem of variable selection
in linear regression were presented in Gnot, Knautz and Trenkler (1994).
The paper Gnot and Grz¸adziel (1997) (Preprint 46 of the Dept.
Math. of the Agricultural Univ. of Wroc![]() aw)
is devoted to the study of the problem of estimating
aw)
is devoted to the study of the problem of estimating ![]() when r>1. In this preprint the convex programming approach developed
by Hartung (1981) (Annals of Statistics 9) for estimating
variance components was used. Positive SemiDefinite Minimium Biased (PSDMB)
estimator of
when r>1. In this preprint the convex programming approach developed
by Hartung (1981) (Annals of Statistics 9) for estimating
variance components was used. Positive SemiDefinite Minimium Biased (PSDMB)
estimator of ![]() was
defined and characterized by a set of nonlinear equations.
was
defined and characterized by a set of nonlinear equations.
Solving this set of equations could be reduced to a nonconvex, nonsmooth
optimization problem which can be solved by global optimization procedures.
During the PhD Students Session I am going to discuss the efficiency of
the algorithm finding the unique solution of this problem. Finally I want
to present some alternative estimators of ![]() and compare them with the PSDMB estimator of
and compare them with the PSDMB estimator of ![]() .
.
The degree of grinding of mechanical pulp, which is used in papermaking, is usually described by the so-called Freeness-number. Besides Freeness meters used for analysing pulp, these have also appeared optical fiber-length meters. Nowadays it is unclear if there is any use for these optical fiber length meters in analysing the quality of pulp. Fiber length meters give results in the form of a histogram of fiber lengths in predefined classes.
In this paper generalized linear models were used to modeling the distribution of mechanical pulp fiber length. The results of a mechanical pulp's end grinder test drive were modeled with generalized linear models. Each pulp's samples were measured with Kajaani FS-200 fiber length meter. The fiber length distribution was modeled with generalized linear models by using the energy specific consumption (ESC) of the end grinder for the explanatory variable. The other quality properties of mechanical pulp can be further modeled with this modeled fiber length distribution.
From the results we can see that generalized linear models are very
suitable for modeling the fiber length distribution of mechanical pulp
and they explain very well the properties of mechanical pulp, even better
than the usually used Freeness-number.
We examine a 1918 inequality of Julius von Szökefalvi Nagy [Gyula
Szokefalvi-Nagy] and some 1935 extensions of Tiberiu Popoviciu concerning
the standard deviation and range of a set of real numbers and some equivalent
inequalities for the Studentized range due to Keshavan Raghavan Nair (1947,
1948) and George William Thomson (1955). We also examine some closely related
inequalities due to Bhatia and Davis (1999), Guterman (1962), and Margaritescu
and Voda (1983). We survey the literature and give various extensions and
applications in statistics and matrix theory. We also include some historical
and biographical information and present an extensive bibliography with
over 225 entries.
* Joint work with George P. H. STYAN
(McGill University, Montréal, Canada). Part of an MSc thesis at
McGill University.
Models for mixtures of ingredients are typically fitted by Scheffé's canonical model forms. Draper and Pukelsheim (1998) have suggested an alternative class of so called K-models based on the Kronecker algebra of vectors and matrices.
The design problem for these models has been solved only partially so far. For the first-degree and second-degree cases, Draper and Pukelsheim (1998) and Draper, Heiligers, and Pukelsheim (1998) have identified a set of designs which is a minimal complete class with respect to the Kiefer ordering of moment matrices.
Starting from this result, the problem of finding ![]() -optimal
designs for second-degree K-models is explored. In the case of two or three
ingredients, such
-optimal
designs for second-degree K-models is explored. In the case of two or three
ingredients, such ![]() -optimal
designs are already known. Current research is devoted to the case of four
or more ingredients.
-optimal
designs are already known. Current research is devoted to the case of four
or more ingredients.
References
Draper, N. R., Heiligers, B. and Pukelsheim, F. (1998). Kiefer ordering of simplex designs for second-degree mixture models with four or more ingredients. Report No. 403, Institut für Mathematik, Universität Augsburg.
Draper, N. R. and Pukelsheim, F. (1998). Mixture models
based on homogeneous polynomials.
Journal of Statistical Planning and
Inference, 71, 303-311.
This topic concerning three special subjects:
(A) Admissibility of linear estimators in linear models.
The admissibility of linear estimator is characterized in the model ![]()
![]() in the cases: (i)
in the cases: (i) ![]() ,
while
,
while ![]() with a ellipsoidal constraint
with a ellipsoidal constraint ![]() ,
where N is known nonnegative definite matrix, or (ii)
,
where N is known nonnegative definite matrix, or (ii) ![]() with inequlity constraints, that is
with inequlity constraints, that is ![]() ,
where
,
where ![]() is a known
is a known ![]() matrix},
matrix},![]() is a given set of nonnegative definite matrices of order n. For
two important special cases , the regression parameter set is unrestricted
or bounded ellipsoid set, therefore, the original results due to Rao (1976)
and Hoffmann (1977) respectively, are unified.
is a given set of nonnegative definite matrices of order n. For
two important special cases , the regression parameter set is unrestricted
or bounded ellipsoid set, therefore, the original results due to Rao (1976)
and Hoffmann (1977) respectively, are unified.
(B) Admissibility of nonnegative quadratic estimators in variance
components models.
The estimation of the vector of variance components under general variance components models with respect to the scale quadratic loss function is consider. A new method of constructing a better estimator and how to deal with the admissibility of quadratic estimator of variance components with the covariance matrix may be singular is presented. Using this method, a necessary condition for admissbility of nonnegatve quadratic estimator is given. For a special case, a necessary and sufficient condition is also given.
(C) Generalized matrices versions of the Wielandt inequality
with some statistical application.
We give an answer of Wang's (1998) conjecture about matrix version of
the Wielandt inequality, and some applications are discussed.
Distance criterion is an optimality criterion in design of experiments.
A design ![]() is said to be at least as good as
is said to be at least as good as ![]() with respect to DS(
with respect to DS(![]() )-criterion
if
)-criterion
if ![]() where
where ![]() and
and ![]() are the estimators corresponding to
are the estimators corresponding to ![]() and
and ![]() ,
respectively. If the design
,
respectively. If the design ![]() is at least as good as any competing design
is at least as good as any competing design ![]() for all
for all ![]() ,
then it is said to be distance optimal (DS-optimal). In other words, a
design is DS-optimal, if the Euclidian distance between the estimator and
the true value is stochastically less than in any competing design. We
have studied the distance criterion in the context of the classical linear
model assuming that the random errors are normally distributed. We found
that in polynomial fit models, there does not usually exist DS-optimal
designs. However, nonsymmetric designs can be improved symmetrizing them.
In the first degree m-way polynomial fit models when the experimental
region is an m-dimensional Euclidian ball or cube, optimal designs
exist and they are orthogonal. We also studied the limiting behaviour of
the DS(
,
then it is said to be distance optimal (DS-optimal). In other words, a
design is DS-optimal, if the Euclidian distance between the estimator and
the true value is stochastically less than in any competing design. We
have studied the distance criterion in the context of the classical linear
model assuming that the random errors are normally distributed. We found
that in polynomial fit models, there does not usually exist DS-optimal
designs. However, nonsymmetric designs can be improved symmetrizing them.
In the first degree m-way polynomial fit models when the experimental
region is an m-dimensional Euclidian ball or cube, optimal designs
exist and they are orthogonal. We also studied the limiting behaviour of
the DS(![]() )-criterion
as
)-criterion
as ![]() tends to 0 or
tends to 0 or ![]() .
.
We apply the local influence approach to the identification of influential
observations in classification problems. Our main interest is in the posterior
probabilities of group membership and in the atypicalities corresponding
to a set of unclassified observations. Different perturbation schemes to
extract influential data are applied and several ways to measure influence
on various aspects of the classification results are suggested. We present
expected influence measures for situations where no particular set of unclassified
data has been specified. Three ways to calculate such expectations are
compared. The proposed methods can be applied to discriminant analysis
based on predictive densities and to results calculated from estimative
densities. The group dependent sampling distributions are assumed to be
multivariate normal distributions with either equal or unequal covariance
matrices. Covariate adjusted classification problems are also considered.
Most of the results we discuss involve eigenanalysis of a matrix which
can be written out in a compact and interpretable way.
In this paper I will compare three different grouping analyses by doing cluster analyses for data where there are 6700 patients who have risk of coronary heart disease. I have first performed the well known K-Means Cluster analysis; the results supported well the predictions made by the doctors. After that I have used two different network application for the data: Kohonen's Self-Organizing Maps and Bayesian network modelling. Bayesian modelling has been developed in the Helsinki University of the Department of Computer Science and Self-Organizing Maps in the Helsinki University of Technology.
In the Bayesian network modelling we select first the model structure which can, for example, be the structure of a neural network. Then we order the structure's parameters. When selecting structure and parameters we use as a learning criteria Bayesian posterior probability.
In the Kohonen's neural network R-dimensional input data is mapped
onto two-dimensional neural level. With every node i a parametric
reference vector m is associated. An input vector is compared with
the m and the input is mapped to the best matched node i.
Values of the reference vector m change towards the values of the
input vector which is mapped onto m.
We present a group of universal factorization equalities for ![]() and
and ![]() block matrices, and then use them to establish a variety of equalities
for ranks and determinants of matrices. Based on them, we also establish
a universal factorization equality for real quaternion matrices.
block matrices, and then use them to establish a variety of equalities
for ranks and determinants of matrices. Based on them, we also establish
a universal factorization equality for real quaternion matrices.
* Joint work with George P. H. STYAN
(McGill University, Montréal, Canada). Part of an MSc thesis at
Concordia University.
Let AXB = C is a matrix equation over the field of complex
numbers. We consider under what conditions this equation has ![]() or
or ![]() upper block triangular solutions, and present some special cases related
to generalized inverses of matrices. Moreover, we also consider block triangular
solutions of matrix equations of the form AX
- YB = C and AX -
XB
= C.
upper block triangular solutions, and present some special cases related
to generalized inverses of matrices. Moreover, we also consider block triangular
solutions of matrix equations of the form AX
- YB = C and AX -
XB
= C.
1 Poster.
We derive the expression for the Drazin inverse of a modified matrix.
The perturbation bound for the Drazin inverse is also established, i.e.,
the open problem posed by Campbell and Meyer [in Linear Algebra Appl.,
10(1975)
pp. 77-83] has been partially solved.
(1) In this paper, necessary and sufficient conditions for equalities
between a2y'(I-PX)y
and ![]() under the general linear model, where
under the general linear model, where
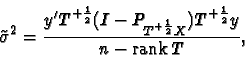
a2 is a known positive number, are derived. Further, when the Gauss-Markov estimators and the ordinary least squares estimators are identical, we obtain a relative simply equivalent condition. At last, this condition is applied to an interesting example.
(2) Consider the partitioned linear 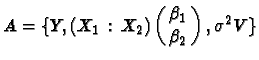 and its five reduced linear models, where
and its five reduced linear models, where ![]() and
and ![]() .
In this paper, the formulas for the differences between the BLUEs of
.
In this paper, the formulas for the differences between the BLUEs of ![]() under A and its BLUEs under reduced linear models of A are
given. Further, the necessary and sufficient conditions for the BLUEs of
under A and its BLUEs under reduced linear models of A are
given. Further, the necessary and sufficient conditions for the BLUEs of ![]() under reduced linear models to be the BLUEs of
under reduced linear models to be the BLUEs of ![]() under A are established. Moreover, we also study the connections
between the MINQUE of
under A are established. Moreover, we also study the connections
between the MINQUE of ![]() under A and the MINQUE of
under A and the MINQUE of ![]() under its reduced linear models.
under its reduced linear models.
(3) The Gauss-Markov estimator of X1BX2'
under the growth curve model ![]() is given. Necessary and sufficient conditions for equality between A1YA2'
and B1YB2', where Ai=Xi(Xi'WiXi)+Xi'Wi, Bi=Xi(Xi'SiXi)+Xi'Si,
with Wi, Si being any matrix, i=1,
2, are derived. Finally, a number of criteria for A1YA2'
to coincide with the Gauss-Markov estimator of X1BX2'
are established.
is given. Necessary and sufficient conditions for equality between A1YA2'
and B1YB2', where Ai=Xi(Xi'WiXi)+Xi'Wi, Bi=Xi(Xi'SiXi)+Xi'Si,
with Wi, Si being any matrix, i=1,
2, are derived. Finally, a number of criteria for A1YA2'
to coincide with the Gauss-Markov estimator of X1BX2'
are established.
(4) This article deals with estimating problems for location (scale) models from grouped samples. Suppose the support region of a density function, which does not depend on parameters, are divided into some disjoint intervals, grouped samples are the number of observations falling in each intervals respectively. The studying of grouped samples may be dated back to the beginning of the century, in which only one sample location and/or scale models is considered. This article considers one sided estimating problems for location models. Some methods for computing the maximum likelihood estimates of the parameters subject to order restrictions are proposed and a numerical example by the method is given.
Some of the above research is joint work with Wei Gao (Northeast Normal
University), Bei-Sen Liu (Tian Jin University), Ning-Zhong Shi (Northeast
Normal University) and Xiang-Hai Zhu (Northeast Normal University).