METSÄTYÖKONESIMULAATTORI
OSA 2
TAUSTATEORIAA JA KÄYTÄNNÖN
ESIMERKKEJÄ
ERKKI MÄKELÄ
![]()
1. JOHDANTO
Tässä metsätyökonesimulaattorin käyttöoppaan toisessa osassa esitellään simulaattorin toiminnan taustalla olevia tilastollisia malleja sekä tarkastellaan muutamia käytännön esimerkkejä.
Luvussa 2 käsitellään runkokäyrän kapeneman ennustamista sekamallin avulla, luvussa 3 metsän generointia todellisesta metsästä tehdyn satunnaisotoksen perusteella ja luvussa 4 puunrungon katkaisua tukeiksi optimaalisella tavalla hinnan perusteella. Luvussa 5 suoritetaan esimerkkiajoja sekä vertaillaan eri ajoparametrien vaikutusta ennusteeseen.
Esimerkkiajojen aineistona käytettiin 200 metsätyökoneen
mittaamaa ja katkomaa kuusta Pohjois-Suomesta. Metsän generointi -modulia
demonstroitaessa käytettiin koko aineistoa ja simulointi-modulia demonstroitaessa sen 50
ensimmäistä runkoa. Aineisto on saatavissa projektin www-sivuilta
<http://www.uta.fi/laitokset/mattiet/tilasto/projekti.html>.
2. SIMULOINTI
Jotta puunrunko onnistuttaisiin katkomaan tukeiksi optimaalisella tavalla, on tunnettava puun runkokäyrä tukkirajalle asti. Metsätyökone tekee rungon tyvipäästä alkaen mittauksia, joiden perusteella se ennustaa loppurungon läpimittaa. Simulaattorissa voidaan valita käytetäänkö puunrungon kapeneman ennustamiseen ensimmäisen, toisen vai kolmannen asteen polynomia.
Simulaattori laskee ennusteet satunnaiskertoimisen regressiomallin avulla. Se on yleisemmän sekamallin erikoistapaus. Laskettaessa ennustetta runkokäyrälle käytetään hyväksi tietoa sekä käsiteltävänä olevasta rungosta (satunnaisvaikutukset) että suuremmasta puujoukosta (kiinteät vaikutukset). Tälläinen malli on muotoa
![]() (2.1)
(2.1)
missä ![]() on
i. puun halkaisija korkeudella
on
i. puun halkaisija korkeudella ![]() ,
, ![]() keskikäyräparametrejä,
keskikäyräparametrejä, ![]() i.
puuhun liittyviä satunnaisvaikutuksia eli poikkeamia keskiparametreista sekä
i.
puuhun liittyviä satunnaisvaikutuksia eli poikkeamia keskiparametreista sekä ![]() mallin satunnaisvirhe, jonka odotusarvo E(
mallin satunnaisvirhe, jonka odotusarvo E(![]() ) = 0. Parametrivektori
) = 0. Parametrivektori ![]() ja
ja ![]() ovat riippumattomia ja normaalisti jakautuneita parametrein N(0,D)
ja N(0,s2),
missä D on q ¥ q-kovarianssimatriisi
ja s2 =
0.
ovat riippumattomia ja normaalisti jakautuneita parametrein N(0,D)
ja N(0,s2),
missä D on q ¥ q-kovarianssimatriisi
ja s2 =
0.
Matriisiesityksenä yleinen sekamalli voidaan lausua muodossa
![]() (2.2)
(2.2)
Jos ![]() sisältää i. rungon mittaukset ja suunnittelumatriisit
sisältää i. rungon mittaukset ja suunnittelumatriisit ![]() ja
ja ![]() ovat muotoa
ovat muotoa
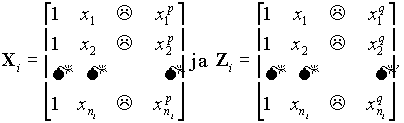
missä q ? p, saadaan malli (2.1). Jos q = p eli Xi = Zi, yhtälö (2.2) supistuu muotoon
![]()
Ennustettaessa runkokäyriä harvesteritilanteessa riittää ennustemalliksi kuusille yleensä 2. asteen polynomi, jossa on mukana kaksi satunnaisvaikutustermiä. Ennusteet voidaan tällöin laskea kaavalla
![]() (2.3)
(2.3)
Simulaattori käyttää kiinteiden vaikutusten parametrien b määrittämiseen annettua määrää mallipuita. Olkoon näiden mallipuiden lukumäärä I. Kiinteiden vaikutusten parametrit rungolle k = I + 1 estimoidaan I:n aikaisemmin käsitellyn rungon mittatiedoista siten, että
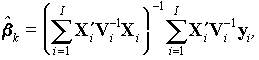 (2.4)
(2.4)
missä ![]() Tämä on BLUE-estimaattori siinä tapauksessa, että D ja s2 tunnetaan.
Käytännössä parametrejä D ja s2 ei kuitenkaan tunneta, vaan ne estimoidaan
aineistosta.
Tämä on BLUE-estimaattori siinä tapauksessa, että D ja s2 tunnetaan.
Käytännössä parametrejä D ja s2 ei kuitenkaan tunneta, vaan ne estimoidaan
aineistosta.
Merkitään rungon k tunnettuja mittauksia vektorilla yk(1). Satunnaisvaikutusten parametrit voidaan estimoida nyt kaavalla
![]() . (2.5)
. (2.5)
Estimoituaan parametrit simulaattori laskee ennusteen rungon tuntemattoman osan kapenemiselle ja määrittää puusta saatavan hinnan maksimoivat katkaisukohdat luvussa 4 esitetyllä tavalla. Simulaattori suorittaa katkaisun ja "mittaa" puunrunkoa eteenpäin annetun matkan, minkä jälkeen satunnaisvaikutusten parametrit bk päivitetään ja lasketaan uusi ennuste sekä uudet optimaaliset katkaisukohdat.
Ennustetun ja todellisen runkokäyrän välistä virhettä mitataan RMSE:llä (root mean square error)
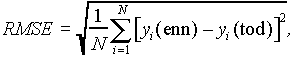
missä N on ennusteiden yi
lukumäärä.
![]()
![]()
![]()
Metsää generoitaessa tehdään ensin yksinkertaista
satunnaisotantaa käyttäen halutunkokoinen otos todellisen metsän puista. Tämän
jälkeen määrätään generoinnissa käytettävän polynomin aste p ja lasketaan
pienimmän neliösumman menetelmällä parametrit ![]() otoksen kullekin puulle i siten, että
otoksen kullekin puulle i siten, että
![]() (3.1)
(3.1)
missä
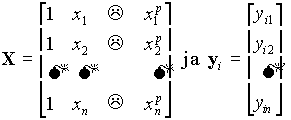 (3.2)
(3.2)
missä puolestaan yin on i. puun rungon läpimitta korkeudella xn.
Parametrien ![]() oletetaan noudattavan moniulotteista normaalijakaumaa siten, että
oletetaan noudattavan moniulotteista normaalijakaumaa siten, että
![]() (3.3)
(3.3)
missä
 (3.4)
(3.4)
Kovarianssimatriisi S voidaan jakaa yksikäsitteisesti Choleskyn hajotelmaan siten, että
![]() (3.5)
(3.5)
missä L on alakolmiomatriisi.
Generoimalla nyt haluttu määrä N(0,Ip)-jakautuneita satunnaislukuvektoreita z saadaan samalla haluttu määrä parametrivektoreita a kaavan
![]() (3.6)
(3.6)
avulla.
Kun näistä generoiduista parametrivektoreista ![]() muodostetaan matriisi A siten,
että
muodostetaan matriisi A siten,
että
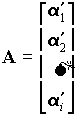 (3.7)
(3.7)
saadaan generoitavan metsän runkokäyrästö Y(enn) yksinkertaisesti kaavalla
![]() (3.8)
(3.8)
Runkokäyrää generoidaan siihen korkeuteen asti, jossa rungon läpimitta alittaa 90 cm.
Tämän jälkeen ohjelma pölkyttää sekä todellisen että generoidun metsän rungot tukeiksi luvussa 4 esitetyllä tavalla ja kerää talteen tiedot tukkien jakaumasta. Ohjelma testaa jakaumien samanlaisuutta toisaalta jakauma-asteella ja toisaalta c2-yhteensopivuustestillä.
Jakauma-aste lasketaan kaavalla
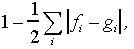 (3.9)
(3.9)
missä summataan yli kaikkien luokkien ja missä fi on 1. jakauman suhteellinen frekvenssi i:nnessä luokassa ja gi 2. jakauman suhteellinen frekvenssi samassa luokassa.
Jakauma-aste saa arvoja väliltä [0,1]. Mitä lähempänä
jakauma-aste on maksimiaan, sitä lähempänä jakaumat ovat toisiaan. Tilanteessa, jossa
jakaumat ovat täysin identtiset, itseisarvojen summaksi tulee nolla, koska fi = gi kaikilla i:n arvoilla, ja
jakauma-aste saa siis arvon 1. Tilanteessa, jossa jakaumat ovat täysin erilaiset, on aina
joko fi tai gi nolla ja kahden
jakauman suhteellisten frekvenssien summaksi tulee 2. Siksi tarvitaan kerroin 1/2.
![]()
![]()
![]()
Optimoinnilla tarkoitetaan tässä yhteydessä rungon katkomista tukeiksi siten, että rungosta saatava hinta maksimoituu. Ongelma voidaan esittää suunnattuna graafina, josta etsitään graafin solmujen välinen pisin reitti. Tästä tulee nimitys pisimmän reitin algoritmi (Näsberg 1985), jonka avulla myös Simulaattori laskee optimaaliset katkaisukohdat. Pituus symboloi tässä tukista saatavaa hintaa. Koska käytettävä graafi on asyklinen, saadaan ongelma ratkaistua tehokkaasti.
Olkoon d standardinmukaisten tukkipituuksien suurin yhteinen tekijä (normaalisti 5–10 cm). Rungon hyödynnettävä osa jaetaan N:ään yhtäpitkään d:n pituiseen osaan. Nyt voidaan luoda graafi, jossa on N+1 solmua numeroituina 0:sta N:ään. Solmu i vastaa rungon kohtaa id, jonka oletetaan olevan mahdollinen katkaisukohta. Solmu 0 symboloi tyveä, solmu NT tukkirajaa ja solmu N hyödynnettävän osan korkeutta.
Graafiin liitetään särmä (i,k), jos rungon kohdat id ja kd ovat molemmat mahdollisia katkaisukohtia ja jos on olemassa standardinmukainen tukin pituus lj = (k–i)d. Särmälle annetaan sama arvo kuin vastaavalla tukilla olisi. Hinta määräytyy tukin tilavuuden, laadun, pituuden ja kapeamman pään halkaisija mukaan. Särmien vetämisessä käytetään apuna tietoa tukkien minimi- ja maksimipituuksista zmin ja zmax.
Koska optimaalinen katkaisu voi tuottaa myös hukkapuuta, vedetään jokaisesta mahdollisesta tukin päätössolmusta särmä viimeiseen solmuun N. Näille särmille annetaan arvoksi nolla.
Kun kaikki särmät on vedetty, graafista (kuva 4.1) etsitään pisin eli arvokkain reitti solmusta 0 solmuun N.
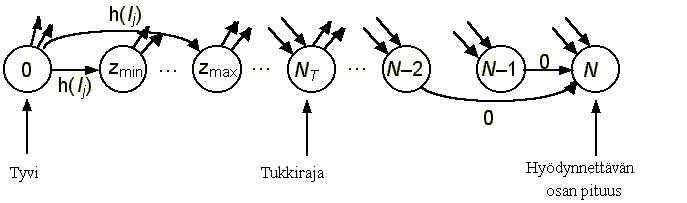
Kuva 4.1. Pisimmän reitin verkko (h(lj) on tukin hinta)
![]()
5.1. Ajoparametrit ja RMSE
Simulaattorissa on mahdollista suorittaa ajoja erilaisilla asetuksilla. Voidaan valita mm. ennustepolynomin aste, ennustepolynomissa käytettävien satunnaisvaikutustermien lukumäärä, ennustamisessa huomiotta jätettävän tyviosan pituus sekä pituus, jonka jälkeen Simulaattori laskee seuraavan katkaisukohdan. Seuraavassa tarkastellaan eri ajoparametrien vaikutusta RMSE:hen.
Ensin tutkittiin, miten ennustepolynomin aste vaikuttaa ennusteen onnistumiseen esimerkkiaineistossa. Tulokset on esitetty kuvassa 5.1. Käytettäessä 1. asteen polynomia RMSE sai suurempia arvoja ja myös sen keskihajonta oli suurempaa kuin käytettäessä 2. asteen polynomia. Varsinkin 3. katkaisun kohdalla ero oli huomattava. 3. asteen termin lisääminen 2. asteen polynomiin ei enää parantanut ennusteiden tarkkuutta tässä aineistossa, vaan sekä RMSE:n keskiarvo että hajonta kasvoivat hieman.
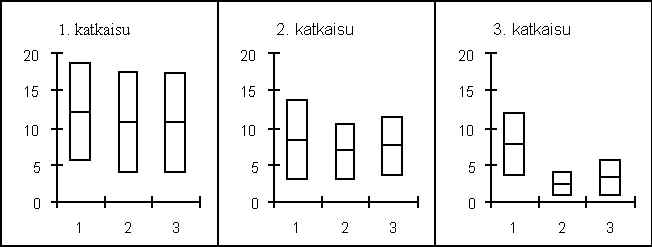
Kuva 5.1. RMSE:n keskiarvo ja hajonta vs polynomin aste
Esimerkkiaineistossa ennusteet onnistuivat siis parhaiten käytettäessä 2. asteen polynomia. Tällaisessa polynomissa voidaan käyttää enintään kolmea satunnaisvaikutustermiä. Seuraavaksi tutkittiin, miten satunnaisvaikutustermien lukumäärä vaikuttaa RMSE:hen.
Jos satunnaiskertoimet jätetään pois, ennustamisessa ei voida käyttää lainkaan hyväksi käsiteltävästä puusta mitattavaa tietoa, vaan ennustaminen tapahtuu kokonaan aiemmin mitatuista rungoista laskettujen keskiarvoparametrien avulla. Metsän puut ovat kuitenkin iältään ja kasvutavaltaan yksilöitä. Kun se jätettiin huomioimatta, ennusteet epäonnistuivat pahasti, kuten kuvasta 5.2 nähdään.
Jo ennustepolynomin vakiotermin korjaaminen satunnaisvaikutustermillä korjasi tilannetta merkittävästi. Sekä 1. että 2. katkaisussa RMSE laski kolmasosaan. Lisättäessä satunnaiskertoimia myös polynomin muihin kertoimiin tilanne ei muuttunut enää yhtä selvästi. 1. katkaisussa useampien satunnaiskertoimien käyttöönotto ei parantanut ennusteita lainkaan. 2. katkaisussa ennusteet paranivat jonkin verran. 3. katkaisun kohdalla yhden satunnaiskertoimen käyttö ei parantanut ennusteita vielä niin selvästi kuin aikaisempien katkaisujen kohdalla. Toisen satunnaiskertoimen mukaanottaminen pienensi myös 3. katkaisun RMSE-arvot kolmasosaan.
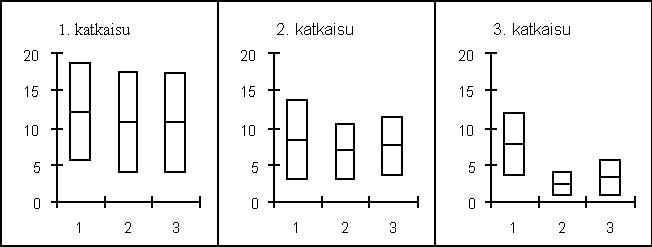
Kuva 5.2. RMSE:n keskiarvo ja hajonta vs satunnaisvaikutustermien lkm
Edellä esitetyn ja aiempien tutkimusten perusteella näyttää siltä, että 2. asteen polynomi korjattuna kahdella satunnaisvaikutustermillä antaa parhaat ennusteet kuusille. Ennusteen tarkkuuteen vaikuttaa myös rungon tyviosa. Tyvi on usein muodoltaan epäsäännöllinen. Paksutyvinen puu ei välttämättä ole pitkä. Kuvasta 5.3 nähdään, kuinka rungon läpimitta eri korkeuksilla korreloi rungon pituuden kanssa esimerkkiaineistossa. Alimmillaan korrelaatiokerroin on 90 cm korkeudella (0,34).
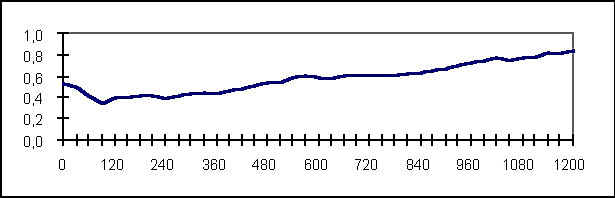
Kuva 5.3. Runkojen läpimittojen korrelaatiot pituuden kanssa 12 metriin asti
Siksi ennustetta laskettaessa onkin usein järkevää jättää tyviosa pois. Kuvassa 5.4 esitetään, kuinka RMSE käyttäytyi, kun tyvestä pois jätettävää osuutta vähitellen pidennettiin. RMSE 1. katkaisukohdassa pieneni tasaisesti 120 cm korkeudelle asti, jonka jälkeen se vakiintui. Tyviosan ennustetta häiritsevä vaikutus ei ulottunut enää 2. katkaisukohdassa laskettuun ennusteeseen.
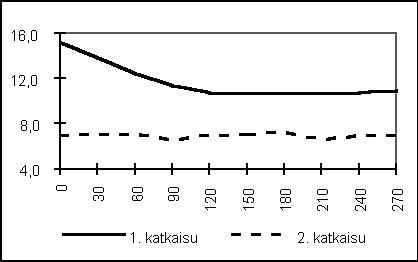
Kuva 5.4. RMSE ja tyvestä poisjätetty osa
Tyven halkaisijan ja RMSE:n korrelaatio on 0,63. Halkaisijan ja RMSE:n korrelaatio pienenee korkeuden kasvaessa. 1,2 metrin korkeudella se on 0,45. Täytyy muistaa kuitenkin, että sekä RMSE että tyven halkaisija ovat molemmat riipuvaisia puun koosta yleensäkin.
Mitä pitemmälle runkoa mitattiin ennenkuin ennuste laskettiin ja katkaisu suoritettiin, sitä paremmin ennusteet onnistuivat kuten oli odotettavissakin. Tulokset on esitetty kuvassa 5.5. RMSE laski sekä 1. että 2. katkaisun kohdalla tasaisesti. Ajoja suoritettiin 30 cm välein.
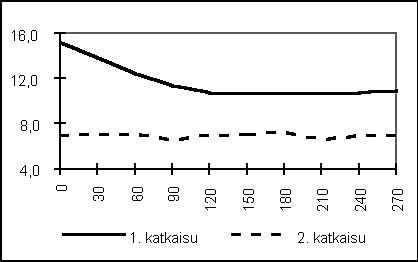
Kuva 5.5. RMSE ja tunnetun osan pituus
5.2. Simuloinnin tuloksia
Esimerkkiajo suoritettiin Simulaattorin oletusarvojen mukaisesti luvussa 5.1 esitettyjen tulosten vahvistettua niiden soveltuvan parhaiten myös 50 kuusesta koostuvaan esimerkkiaineistoon. Ennustepolynomi alustettiin 20 ensimmäisen rungon avulla ja ennusteiden onnistumista tutkittiin loppujen 30 rungon kohdalla. Esimerkkiajon tuloksia on esitelty sivuilla 10–11 taulukossa 5.1 ja kuvissa 5.6 ja 5.7.
Ennusteen onnistumisen mittana käytetään RMSE:n ohella tappiofunktiona optimaalisen ja ennusteen mukaan lasketun hinnan erotusta sekä suhteellista hintaa. Syntynyt tappio ja suhteellinen hinta eivät ole suoraan riippuvaisia RMSE:stä. Laskettaessa hinnat hintamatriisista pienikin virhe ennusteessa saattaa koitua kalliiksi, jos sen vuoksi viimeinen tukki jää hieman minimivaatimusta lyhyemmäksi. Toisaalta katkaisuvaihtoehtoja on paljon ja niistä voi useampikin tuottaa hyvän lopputuloksen. RMSE:n ja tappion välinen korrelaatio on 0,35 sekä RMSE:n ja suhteellisen hinnan yllättäen 0,005.
Ennusteet onnistuivat lyhyille rungoille, joita oli 14 kappaletta, lähes poikkeuksetta erittäin hyvin. Puolella näistä lyhyistä rungoista optimaaliset ja ennusteen perusteella lasketut katkaisukohdat olivat täysin samat ja muulloinkin tappio jäi melko pieneksi. Poikkeuksena oli runko 23. Vaikka sen RMSE olikin pieni, tappiosta tuli huomattavan suuri. Tämä johtuu siitä, että rungon alaosassa oli jotain epäsäännöllisyyttä, minkä vuoksi tukkirajan ennustettiin olevan hieman korkeammalla kuin se todellisuudessa oli. Ensimmäinen tukki katkaistiin siten liian pitkäksi. Toista tukkia ei enää saatu ja tukkipuuksi kelpaavaa puuta jäi hyödyntämättä lähes kolme metriä.
Myös pitkillä rungoilla suuren tappion syynä oli kaikissa tapauksissa se, että tukkirajan oltiin ennustettu olevan hieman korkeammalla kuin se todellisuudessa oli. Tällaisessa tilanteessa toiseksi viimeinen katkaisu tehtiin liian myöhään ja loppu runko jäi hukkapuuksi. Tästä ovat hyviä esimerkkejä rungot 16, 19, 23, 25 ja 30. Runkojen 23 ja 25 tapauksessa viimeinen tukki saatiin kyllä katkaistua Simulaattoriin ohjelmoitujen ehtojen mukaisesti. Saadun tukin hinta oli kuitenkin hintamatriisissa nolla.
Tappiota syntyy myös, jos tukkirajan ennustetaan olevan matalammalla, kuin se on todellisuudessa. Tällöin ensimmäinen ja arvokkain tukki katkaistaan liian lyhyeksi, kuten kävi rungon 4 tapauksessa. Tällaisessa tilanteessa syntynyt tappio jäi kuitenkin pienemmäksi kuin tapauksessa, jossa osa puusta jäi hyödyntämättä.
Taulukko
5.1. Esimerkkiajon tulokset (optimaalinen arvo
suluissa)
Katkaisu |
||||||||||||
I |
II |
III |
IV |
|||||||||
Runko |
Pituus |
RMSE |
Pituus |
RMSE |
Pituus |
RMSE |
Pituus |
Tappio |
Suht. hinta | |||
1 |
570(510) | 14,7 | 540(510) | 19,9 | 390(480) | 0,0 | 7 |
0,98 |
||||
2 |
570(570) | 12,9 | 330(330) | 0,0 | 0 |
1,00 |
||||||
3 |
510(510) | 7,5 | 540(540) | 4,3 | 0 |
1,00 |
||||||
4 |
540(570) | 11,5 | 510(570) | 7,5 | 510(420) | 2,6 | 15 |
0,97 |
||||
5 |
540(540) | 5,8 | 570(390) | 7,5 | – (330) | 9 |
0,96 |
|||||
6 |
570(480) | 6,0 | 420(510) | 3,5 | 0 |
1,00 |
||||||
7 |
540(540) | 18,6 | 510(330) | 14,7 | 330(510) | 0,0 | 6 |
0,98 |
||||
8 |
510(330) | 22,4 | 390(570) | 13,7 | 540(540) | 8,4 | 14 |
0,96 |
||||
9 |
510(390) | 10,2 | 540(510) | 7,8 | 450(540) | 2,9 | 4 |
0,99 |
||||
10 |
510(570) | 26,5 | 570(570) | 6,2 | 390(330) | 0,0 | 10 |
0,97 |
||||
11 |
540(570) | 5,7 | 570(540) | 9,7 | 3 |
0,99 |
||||||
12 |
540(570) | 6,2 | 570(540) | 4,0 | 10 |
0,96 |
||||||
13 |
570(570) | 4,7 | 450(450) | 2,4 | 0 |
1,00 |
||||||
14 |
540(570) | 12,7 | 330(390) | 7,1 | 420(330) | 0,0 | 5 |
0,98 |
||||
15 |
570(540) | 8,4 | 510(570) | 17,2 | 540(510) | 3,3 | 11 |
0,97 |
||||
16 |
510(540) | 32,4 | 390(360) | 14,1 | 390(330) | 4,0 | – (330) |
26 |
0,94 |
|||
17 |
330(330) | 3,4 | 420(420) | 0,0 | 0 |
1,00 |
||||||
18 |
540(330) | 14,6 | 330(540) | 7,7 | 330(330) | 0,0 | 5 |
0,98 |
||||
19 |
570(450) | 7,4 | 480(510) | 6,3 | – (360) | 31 |
0,90 |
|||||
20 |
510(420) | 5,8 | 420(510) | 0,0 | 6 |
0,96 |
||||||
21 |
510(540) | 8,0 | 540(510) | 4,0 | 3 |
0,98 |
||||||
22 |
540(330) | 5,6 | 540(420) | 2,5 | – (330) | 9 |
0,95 |
|||||
23 |
540(390) | 3,9 | – (420) | 23 |
0,80 |
|||||||
24 |
510(390) | 3,8 | 450(570) | 0,0 | 11 |
0,92 |
||||||
25 |
540(540) | 12,3 | 510(390) | 6,3 | 300(420) | 0,0 | 25 |
0,93 |
||||
26 |
570(570) | 4,7 | 570(570) | 3,2 | 0 |
1,00 |
||||||
27 |
570(540) | 8,5 | 330(330) | 7,0 | 300(330) | 0,0 | 29 |
0,89 |
||||
28 |
570(570) | 4,6 | 540(540) | 4,7 | 0 |
1,00 |
||||||
29 |
540(480) | 11,5 | 420(480) | 0,6 | 8 |
0,95 |
||||||
30 |
510(420) | 24,0 | 390(390) | 20,2 | 570(390) | 11,8 | – (390) |
22 |
0,94 |
|||
ka. |
10,8 | 6,9 | 2,5 | 9,7 |
0,94 |
|||||||
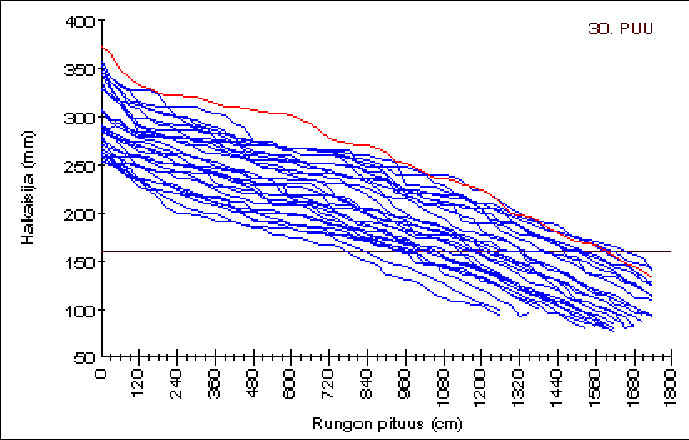
Kuva 5.6. Esimerkkiajon runkokäyrästö
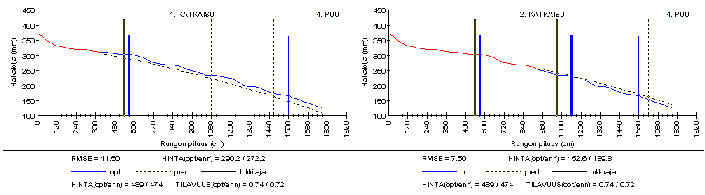
Runko 4: Runko ennustettiin liian lyhyeksi. Seurauksena ensimmäinen tukki katkaistiin hieman liian lyhyeksi. Tappio: 15.
Runko 15: Runko on epäsäännöllisen muotoinen 10 metrin korkeudella heti toisen ennusteen laskemiskohdan jälkeen. Seurauksena RMSE kasvaa kaksinkertaiseksi verrattuna ensimmäiseen katkaisukohtaan. Tappio: 11.
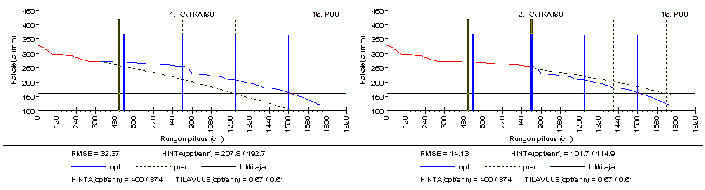
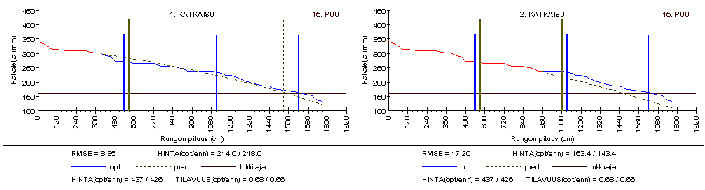
Runko 16: RMSE on erittäin suuri. Rungon alaosa on epäsäännöllinen. Lisäksi se kapenee voimakkaasti 9,5 metrin korkeudella. Toisen katkaisun kohdalla runko ennustetaan paljon pitemmäksi kuin se todellisuudessa on. Tappio: 26.
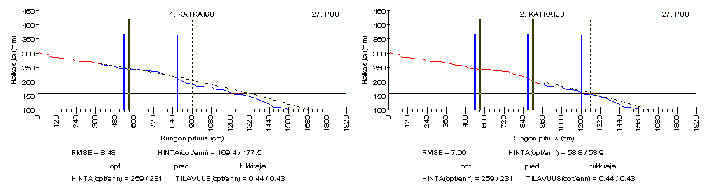
Runko 27: Ennuste onnistui hyvin ja RMSE on pieni. Noin 10 metrin korkeudella runko kapenee kuitenkin hieman voimakkaammin ja runko ennustettiin hiukkasen liian pitkäksi. Tappio: 29.
Kuva 5.7. Esimerkkejä ennusteista
Kuvassa 5.8 on esitetty optimaaliset ja ennusteen mukaan saadut tukkijakaumat. Simulaattori on pyrkinyt katkaisemaan ensimmäisen ja kolmannen tukin selvästi pitemmäksi kuin se olisi katkaistu optimaalisessa tapauksessa. Jakauma-asteet 1., 2. ja 3. katkaisun kohdalla ovat 0,63, 0,85 ja 0,56.
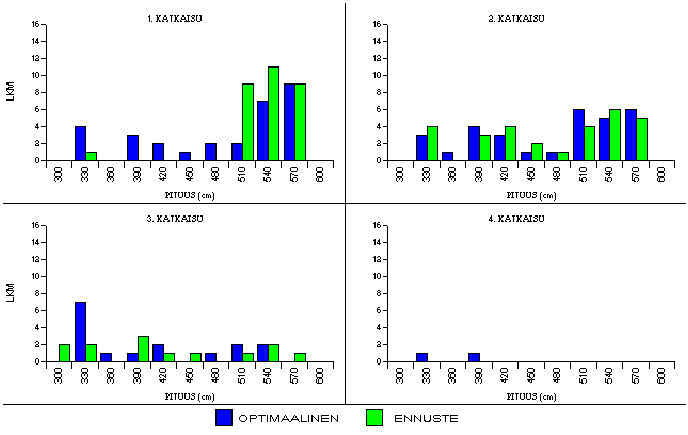
Kuva 5.8. Tukkien pituusjakaumat
Esimerkkiaineiston perusteella vaikuttaa siltä, että tukkipuuksi kelpaavan rungon osan ennustaminen liian pitkäksi on pahempi virhe kuin sen ennustaminen liian lyhyeksi. Jälkimmäisessä tapauksessa metsätyökone voi suorittaa viimeisen katkaisun vasta oikealla tukkirajalla ennusteesta välittämättä, joten koko tukkipuuksi kelpaava runko tulee hyödynnettyä. Todellisuudessa tilanne ei ole kuitenkaan aivan näin yksinkertainen. Vaikka puun yläosasta ei saataisikaan enää tukkia, kelpaa se kuitenkin todennäköisesti ainakin kuitupuuksi, mikä pienentää syntynyttä tappiota.
Virheet ennusteisiin syntyvät ennustettamattomissa olevista
epäsäännöllisyyksistä runkokäyrissä. Ne voivat johtua esimerkiksi mittavirheistä,
oksakohdista tai epäsäännöllisestä kasvutavasta. Mittavirhettä on syytä epäillä
silloin, kun runkokäyrässä on pitkä jakso, jossa runko ei kapene lainkaan.
Metsätyökoneen mittauslaitteen pyörät ovat tällöin saattaneet pyörähtää tyhjää
hypätessään oksakohdassa tai luistaa liukkaalla rungolla.
5.2. Metsän generoinnin tuloksia
Esimerkkiajo suoritettiin ottamalla 200 kuusen runkokäyrästä 20
rungon otos, josta sitten generoitiin 200 runkokäyrää. Ennustepolynomina käytettiin 2.
asteen polynomia ja tukkien hinnat laskettiin hintamatriisista.
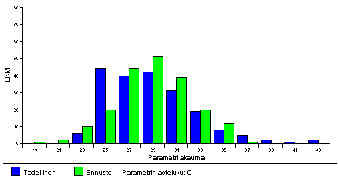 Kuva 5.9. 0. asteen parametri
Kuva 5.10. 1. asteen parametri
Kuva 5.11. 2. asteen parametri |
Generoinnissa oletetaan, että
runkokäyrien parametrit ovat normaalisti jakautuneita. Todellisuudessa ne eivät
kuitenkaan noudata normaalijakaumaa. Varsinkin 0. asteen termi eli vakiotermi noudattaa
pikemmin beta- tai Weibull-jakaumaa. Normaaliapproksimaatio riittää kuitenkin antamaan
suhteellisen hyviä tuloksia. Lisäksi sen etuna on yksinkertaisuus. Moniulotteisesen
normaalijakauman käsittely on huomattavasti ongelmattomampaa kuin moniulotteisen beta-
tai Weibull-jakauman. Kuvissa 5.9 – 5.11 on esitetty esimerkkiajon parametrien jakaumat ja taulukossa 5.2 parametreihin liittyviä tunnuslukuja ja testituloksia. Koska generoitujen runkokäyrien parametrit ovat normaalisti jakautuneita, voidaan jakaumien c2-yhteensopivuustestin p-arvoja käyttää tässä tapauksessa myös todellisten parametrien normaalijakautuneisuuden testaamiseen tietyin varauksin. 0. asteen termin eli vakiotermin p-arvo on hyvin pieni ja niin on syytä epäillä todellisten parametrien normaalisuutta myös esimerkkiaineistossa. |
|||||||
c2 |
df |
p |
Tod. |
Otos |
Enn. |
|||
0. aste |
21,7 |
7 |
0,003 |
keskiarvo |
28,98 | 29,20 | 28,84 | |
hajonta |
3,76 | 3,23 | 3,18 | |||||
1. aste |
13,2 |
8 |
0,106 |
keskiarvo |
–0,83 | –0,83 | –0,81 | |
hajonta |
0,36 | 0,37 | 0,41 | |||||
2. aste |
10,6 |
7 |
0,156 |
keskiarvo |
–0,03 | –0,03 | –0,03 | |
hajonta |
0,02 | 0,02 | 0,02 | |||||
Taulukko
5.2. Parametrien tunnusluvut ja c2-yhteensopivuustestin
tulokset.
| Runkokäyrän parametreistä kuvaa 0.
asteen termi parhaiten niin puun pituuden kuin läpimitankin suuruusluokkaa. Se korreloi
voimakkaasti nimenomaan läpimitan kanssa, kuten kuvan 5.12 pisteparvesta, joka kuvaa 0.
asteen termin sekä puun läpimitan suhdetta 130 cm korkeudella, voidaan nähdä. Verrattaessa generoidun runkokäyrästön läpimittojen jakaumia alkuperäisen aineiston läpimittojen jakaumiin vaikuttaa siltä, että kuten 0. asteen termin jakauma eivät myöskään todellisten runkojen läpimitat noudata normaalijakaumaa. Jakaumat ovat vinoja verrattuna teoriassa normaalisti jakautuneiden, generoitujen runkokäyrien läpimittojen jakaumiin. Jakaumien samanlaisuutta testattaessa saadut p-arvot 0,118 ja 0,071 ovat pienehköjä, mutta niiden avulla ei voi kuitenkaan tulkita jakaumien eroavan toisistaan ratkaisevasti. Kuvissa 5.13 ja 5.14 on esitetty tilanne 130 ja 600 cm korkeuksilla. Kuvassa 5.15 esitetyt tukkirajan korkeuden jakaumat ovat hyvin samanlaiset niin silmämääräisesti kuin testisuureittenkin avulla tarkastellen. Testin p-arvo oli 0,399. Kuvassa 5.16 on esitetty hyödynnettävän osan pituuden jakaumat. Testin p-arvo on 0,000. Sen mukaan jakaumat eivät olisi yhteensopivat. Silmämääräisesti tarkastellen ero ei kuitenkaan vaikuta kovin suurelta. Generoidut rungot ovat jonkin verran pitempiä kuin todelliset. Tämä johtuu osittain siitä, ettei esimerkkiaineiston kaikkia runkokäyriä ole esitetty eksplisiittisesti hyödynnettävän osan loppuun asti. |
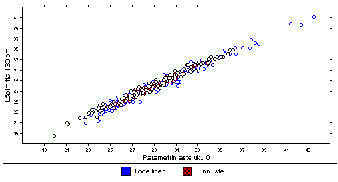 Kuva 5.12. 0. asteen termi ja läpimitta
Kuva 5.13. Läpimitta 130 cm korkeudella
Kuva 5.14. Läpimitta 600 cm korkeudella
Kuva 5.15. Tukkirajan pituus
Kuva 5.16. Hyödynnettävän osan pituus |
Tarkastellaan lopuksi vielä todellisesta ja generoidusta aineistosta saatuja tukkijakaumia. Graafisesti tarkastellen (kuva 5.11) näyttää siltä, että normaalijakaumaan perustuva generointi tuotti melko hyvän tuloksen. Tukkien pituusjakaumat ovat kaikkien katkaisujen kohdalla melko samanlaiset. Todellisen metsän tukeista saatu hinta oli 49177 ja generoidusta 47298. Eroa syntyi 1879 eli 3,8 %.
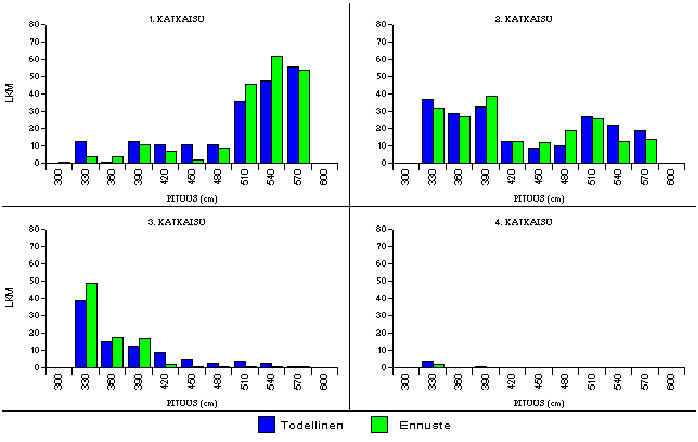
Kuva 5.17. Todellisesta ja generoidusta aineistosta saadut tukkijakaumat
![]()
6. KEHITYSIDEOITA
Metsätyökoneiden suunnittelijoita kiinnostaa tällä hetkellä erityisesti jakauma-apteeraus eli se, kuinka leimikko saataisiin katkottua tukeiksi siten, että tukeille etukäteen asetetut pituus- ja läpimittavaatimukset täyttyisivät. Toinen ajankohtainen aihe on männyn kuivaoksa- ja tuorelatvusrajojen ennustaminen. Parhaillaan selvitetään sitä, miten jakauma-apteeraus ja laaturajojen ennustaminen voitaisiin toteuttaa Simulaattorissa. Tavoitteena on myös lisätä Simulaattoriin metsän spatiaalista generointia suorittava moduli. Spatiaalisuudella tarkoitetaan tässä yhteydessä sitä, miten puut sijaitsevat metsässä.
Käynnissä on myös otantaan liittyvää tutkimusta. Jotta jakauma-apteeraus voitaisiin käytännössä toteuttaa, tarvitaan metsän puista jonkinlainen ennakkoarvio. Lisäksi on tavoitteena selvittää, kuinka mallipuustoa tulisi karsia etukäteen parempien ennusteiden aikaansaamiseksi.
Ennusteita voitaisiin parantaa myös siten, että kun ennusteen
virheen huomataan kasvavan etukäteen asetettua vaatimusta suuremmaksi, ennuste
laskettaisiin välittömästi uudelleen. Nykyisellään Simulaattori päivittää
ennusteet aina vasta edettyään runkoa tietyn matkan.
KIRJALLISUUTTA
Korvenoja, H. & Nummi, T. (1994): Sekamalli rungon kapeneman ennustamisessa metsätyökoneelle. University of Tampere.
Nummi, Tapio (1995): Estimation and prediction in growth curve models with applications. University of Tampere.
Näsberg, Mikael (1985): Mathematical programming models for optimal log bucking. University of Linköping.