 TAMPERE UNIVERSITY OF TECHNOLOGY
-
Department of Signal Processing
TAMPERE UNIVERSITY OF TECHNOLOGY
-
Department of Signal Processing
Introduction |
SoftwareDemonstration software for Matlab |
Results |
People |
Publications |
 |  |  |  |
| available portion of the spectrum (22 radial lines) | Back-projection estimate | Estimate after convergence (exact reconstruction) |
 |  |  |  |
| available portion of the spectrum (11 radial lines) | Back-projection estimate | Estimate after convergence (exact reconstruction) |
 |  | 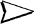 |  |
| available portion of the spectrum (90 degrees aperture, 61 radial lines) | Back-projection estimate | Estimate after convergence (exact reconstruction) |
 |  |  |  |
| available portion of the spectrum (low frequencies) | Back-projection estimate (zero-padding the high frequencies) | Estimate after 62 iterations |

 Information and instructions |
Demonstration software for Matlab (ver. 7.4 or later) 233-kbyte zip-file includes scripts reproducing the above experiments v1.1, released July 23, 2015 | 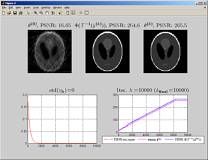 |
 before you proceed with downloading any of the files.
before you proceed with downloading any of the files.
 Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Spatially adaptive filtering as regularization in inverse imaging: compressive sensing, upsampling, and super-resolution”, in Super-Resolution Imaging (P. Milanfar, ed.), CRC Press / Taylor & Francis, ISBN: 978-1-4398-1930-2, September 2010
Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Spatially adaptive filtering as regularization in inverse imaging: compressive sensing, upsampling, and super-resolution”, in Super-Resolution Imaging (P. Milanfar, ed.), CRC Press / Taylor & Francis, ISBN: 978-1-4398-1930-2, September 2010 

 Examples of super-resolution reconstruction as zipped Matlab MAT-files.
Examples of super-resolution reconstruction as zipped Matlab MAT-files. Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Image and video super-resolution via spatially adaptive block-matching filtering”, Proc. Int. Workshop on Local and Non-Local Approx. in Image Process., LNLA 2008, Lausanne, Switzerland, August 2008.
Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Image and video super-resolution via spatially adaptive block-matching filtering”, Proc. Int. Workshop on Local and Non-Local Approx. in Image Process., LNLA 2008, Lausanne, Switzerland, August 2008. Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Image Upsampling Via Spatially Adaptive Block-Matching Filtering”, Proc. 16th European Signal Process. Conf., EUSIPCO 2008, Lausanne, Switzerland, August 2008.
Danielyan, A., A. Foi, V. Katkovnik, and K. Egiazarian, “Image Upsampling Via Spatially Adaptive Block-Matching Filtering”, Proc. 16th European Signal Process. Conf., EUSIPCO 2008, Lausanne, Switzerland, August 2008. Egiazarian, K., A. Foi, and V. Katkovnik, “Compressed Sensing Image Reconstruction via Recursive Spatially Adaptive Filtering”, Proc. IEEE Int. Conf. Image Process., ICIP 2007, San Antonio (TX), USA, pp. 549-552, September 2007.
Egiazarian, K., A. Foi, and V. Katkovnik, “Compressed Sensing Image Reconstruction via Recursive Spatially Adaptive Filtering”, Proc. IEEE Int. Conf. Image Process., ICIP 2007, San Antonio (TX), USA, pp. 549-552, September 2007.